Kaströrelse
Kaströrelse är ganska självbeskrivande. Om ett föremål kastas har föremålet gjort en rörelse som ser ut som en bana. Med hjälp av fysik kan vi titta på rörelsen i detalj och finna var föremålet befinner sig i varje given tidpunkt.
Ett annat vanligt namn är projektilrörelse. Nedanför har vi listat de grundläggande formlerna för kaströrelse. I denna genomgång räknar vi inte med luftmotstånd då det blir för komplicerat.
Sammanfattning av formler för kaströrelse

\[ \begin{matrix} x(t)=v_0\cos{\alpha}t \\ y(t)=v_0\sin{\alpha}t - \frac{gt^2}{2}\\ v_x(t)=v_0\cos{\alpha} \\ v_y(t)=v_0\sin{\alpha} - gt\\ v = \sqrt{v_x^2 + v_y^2} \end{matrix}\]
Där \(v_0\) är utgångshastigheten, \(\alpha\) är elevationsvinkeln, vilket är vinkeln mellan det horisontala planet och utgångshastigheten. Tiden representerar vi med \(t\) och tyngdacceleration för \(g\).
Nedan finns en mer förklarande text om varje formel.
Dela upp rörelsen i x-led och y-led (komposanter)
Vi kommer att dela upp vår kaströrelse i komposanter. Detta gör vi för att det är enklare att studera hur ett föremål rör sig i 1 dimension åt gången än att göra det i båda samtidigt.
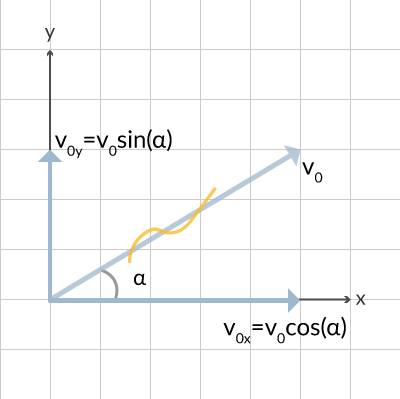
Detta genomförs med hjälp av trigonometri. Den gula ormen talar om att vi ersatt den vinklade hastigheten med två vinkelräta komposanter.
Formler för kaströrelse
När vi delat upp utgångshastigheten \(v_0\) kan vi sätta upp formler för dess position i x- respektive y-led efter en given tidpunkt.
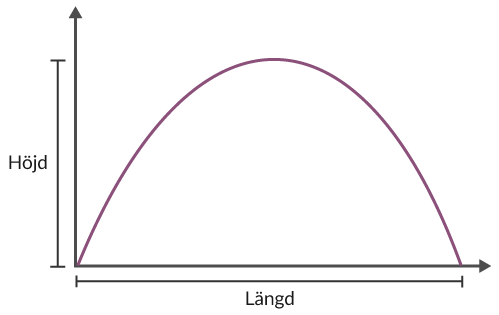
Horisontell sträcka (längd)
Vi kan teckna sträckan horisontellt som förmålet färdats på nedanstående sätt.
\[ x(t) =v_0\cos{\alpha}t\]
Ingen övrig faktor påverkar den vertikala hastigheten, varvid sträckan blir hastigheten i x-led, \(v_0\cos{\alpha}\) multiplicerad med tiden \(t\).
Kortfattat, gravitationen påverkar inte hastigheten i horisontell led.
Vertikal sträcka (höjd)
Den vertikala hastigheten beror däremot på gravitationen.
\[ y(t) =\underbrace{v_0\sin{\alpha}t}_{\text{Uppåt}} ~~~~~ - \underbrace{\frac{gt^2}{2}}_{\text{Gravitation nedåt}}\]
Den första termen, märkt med uppåt kan ses som sträckan bollen färdas med hjälp av den ursprungliga hastigheten \(v_0\).
Den andra termen märkt med gravitation nedåt kan ses som den sträckan som gravitationen dragit ner föremålet.
Beräkna hastigheten i en kaströrelse
Om du behärskar derivator kan du derivera formlerna vi kommit fram till ovan. Om du inte kommit dit ännu i matematiken är det ingen fara.
Horisontell hastighet
Den horisontella hastigheten skrivs som
\[ v_x(t)=v_0\cos{\alpha}\]
och påverkas inte av tiden eller gravitationen. Om vi tittar på den horisontella hastigheten i ett kast kommer den att vara samma oavsett var i kastet vi tittar.
Vertikal hastighet
Den vertikala hastigheten skriver vi som utgångshastigheten uppåt, och sedan subtraherar vi hastigheten gravitationen gett upphov till nedåt.
\[ v_y(t)=v_0\sin{\alpha} - gt\]
Den vertikala hastigheten är tidsberoende, och detta är logiskt då denna förändras. Detta kan vi se när vi kastar exempelvis en boll, först är hastigheten positiv och riktad uppåt. Efter ett tag når bollen sin högsta höjd, och därefter är hastigheten negativ och bollen faller igen.
Ett sätt att beräkna bollens högsta höjd eller vid vilken tidpunkt den är som högst är att frysa ögonblicket då bollen vänder. I detta ögonblick är hastigheten 0.
Beräkna den resulterade hastigheten
Om vi vill beräkna den resulterande hastigheten på bollen får vi slå ihop våra komposanter igen. Detta kan vi göra med Pythagoras sats.
\[ v = \sqrt{v_x^2 + v_y^2}\]
Ett exempel på när den resulterande hastigheten är lämplig är om någon skjuter en fotboll mycket hårt på dig. Det är då en klen tröst att bollen har mycket låg hastighet i vertikal-led.