Newtons gravitationslag
Newtons gravitationslag handlar om att alla partiklar med massa i universum kommer dras mot varandra. Det hela formuleras med följande formel.
\[ F = G\frac{m_1m_2}{r^2}\]
Där \(m_1\) och \(m_2\) är massorna för respektive kropp och \(r\) är avståndet. \(G\) är en konstant med värdet
\[ G = 6.6726\cdot10^{-11} Nm^2/kg^2\]
Om vi illustrerar det bildligt ser det ut som i figur 1.
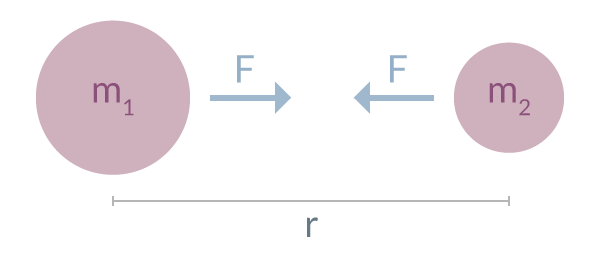
Det är vanligt att \(m_1\) och \(m_2\) betecknas \(m\) och \(M\) istället, men det är ändå samma formel, bara de två olika kropparnas massor kan särskiljas.
Exempel på Newtons gravitationslag
Två astronauter hänger helt vilse, ensamma i rymden en bit ifrån varandra. Vi tänker oss att de är så långt bort i rymden att ingen påverkan från svarta hål, solar, planeter eller någonting annat finns, precis som på bilden nedanför.
Vad händer?
Kraften som verkar mellan de två astronauterna kommer göra att de börjar röra sig mot varandra. Det kommer gå jättesakta men efter ett tag kommer de att stöta i varandra.
Jorden och du
En smått imponerande konsekvens av Newtons gravitationslag är när en människa, förslagsvis du hoppar uppåt. Då drar jorden i dig med lika stor kraft som du drar i jorden med. Då jordens massa är så mycket större än dig kommer jorden i praktiken inte att röra sig närmare dig, utan det är du som får accelerationen.
Exempel på kraft mellan kylskåp och en person
En hörnkyl har en massa på 192 kg. I soffan, 5 meter från kylskåpet ligger en person som har en massa på 95 kg. Hur stor kraft verkar mellan kylskåpet och personen? Bortse från alla övriga inverkande krafter och fenomen.
Detta kan enkelt räknas ut med Newtons gravitationslag.
\[ F = G\frac{m_1m_2}{r^2} = 6.6726\cdot10^{-11}\cdot\frac{192\cdot95}{5^2} = 4.9\cdot10^{-8}~\text{N}=49~\text{nN}.\]
49 nanonewton är en mycket, mycket liten kraft som inte kommer påverka det dagligt livet för personen i soffan. Kylskåpet och personen kommer inte börja röra sig mot varandra då det finns bland annat friktionskrafter som motverkar detta.
Samband med tyngdkraft
Jorden har en massa på ungefär en sexa med 24 nollor efter sig i kg, vilket vi kan hämta ur någon tabell typ Physics Handbook. Vi tänker oss att den ena kroppen i detta fall representeras av jorden med massan
\[ m_1 = 5.977\cdot10^{24}~\text{kg.}\]
Avståndet r mellan dessa kroppar måste vara jordradien (vi använder jordens radie vid ekvatorn i detta fall), vilken är
\[ r = 6378.16~\text{km}.\]
Egentligen så ska vi ha radien från masscentrum på båda kropparna, men vi gör en förenkling och använder bara jordradien vid ekvatorn. Detta kan vi göra eftersom det är sådan liten skillnad om ett föremål som står på jorden har sitt masscentrum flera hundra meter upp när jordradien ändå är så stor. En annan felkälla här är att jorden inte är ett perfekt klot utan mer äggformad, men detta generar inte heller någon större skillnad i vårt slutgiltiga värde.
Den andra massa representeras av en kropp på jorden med massan \(m_2\). Vi vet alltså inte massan på detta objekt. Beräknar vi kraften på som dessa drar med varandra mot får vi följande
\[ F_g = \frac{Gm_1m_2}{r^2}\]
Om vi skriver ovanstående uttryck till
\[ F_g = \Big(\frac{Gm_1}{r^2}\Big) m_2\]
Vi har numeriska värden på uttrycket inom parentes, varvid vi kan beräkna det till
\[ \Big(\frac{Gm_1}{r^2}\Big) = \Big(\frac{6.6726\cdot10^{-11}\cdot{m_1}}{r^2}\Big) \approx 9.81\]
Värdet överensstämmer ganska precis med tyngdaccelerationen för jorden, och enheten som erhålls är dessutom m/s2. Om vi kallar hela ovanstående term för g, så är denna beroende av gravitationskonstanten, jordens radie och jordens massa.
\[ \Big(\frac{Gm_1}{r^2}\Big) = g\]
Vi sätter in det i vårt ursprungliga uttryck och erhåller
\[ F_g = gm_2\]
Där \(m_2\) oftare skrivs som bara \(m\). Om vi byter plats på \(g\) och \(m\) så erhålls nu den välkända formeln för tyngdkraft,
\[ F_{mg} = mg.\]