Effekt för att lyfta ringarna till midsommarstången

Hej! Idag är det midsommarafton 2017. Det firar vi förutom med sedvanlig dans runt midsommarstången även med en relevant uppgift.

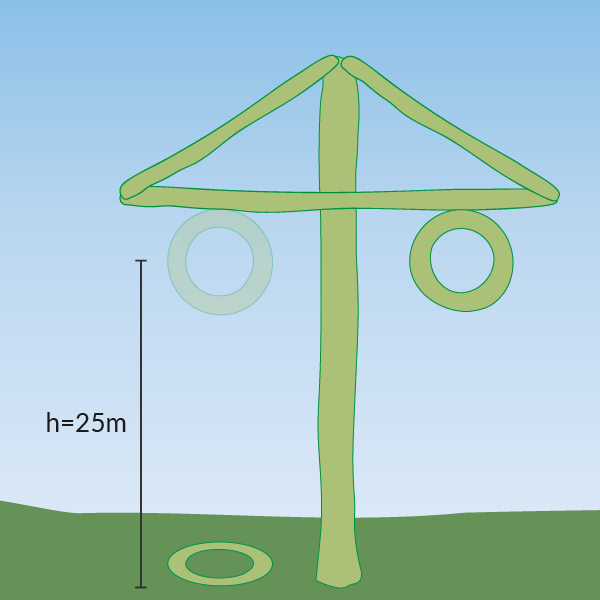
Pelle och Anna har fått tag i en björk som är 30 meter hög. På 25 meters höjd ska det sitta varsin ring på varje sida som vardera har massan 13 kg.

Den första ringen lyfter de upp med hjälp av snören och det hela tar 15 minuter. Vilken effekt har har Pelle och Anna?

Pelle är en hästkille och har turligt nog med sig sin Nordsvenska brukshäst. Hur lång tid tar lyftet med hästen? Anta att en Nordsvensk brukshäst utvecklar en hästkraft.

I båda fallen kommer vi bortse från eventuella friktionsförluster och annat.

Pelle och Anna lyfter ringen

Om vi inte kommer ihåg vad effekt är kan vi fräscha upp minnet under effekt, men riktigt snabbt är det arbete dividerat på tid.

\[ P = \frac{W}{t}\]

Där \(W\) är lägesenergin ringen har när den hänger på höjden 25 meter. Detta skrivs som

\[ W = mgh.\]

Substitutera in detta i uttrycket för effekt.

\[ P = \frac{mgh}{t}\]

Vi sätter in våra värden för massan, tyngdaccelerationen, höjden och tiden. Minuterna multiplicerar vi med \(60\) för att få antalet sekunder.

\[ P = \frac{13\cdot9.82\cdot25}{15\cdot60} \approx 3.5~\text{W}\]

Pelle och Anna utvecklar ungefär 3.5 watt då de drar upp den ena ringen.

Nordsvensk brukshästkraft

Vi utgår från samma uttryck för effekt, fast denna gång är vi intresserade av tiden givet att vi vet effekten \(P\).

\[ P = \frac{mgh}{t}\]

Tiden \(t\) kan lösas ut.

\[ t = \frac{mgh}{P}\]

En hästkraft motsvarar \(P = 735.49875~\text{W}\). Sätts detta in i uttrycket för tiden ges en tid.

\[ t =\frac{13\cdot9.82\cdot25}{735.49875} \approx 4.3~\text{s}.\]

Hästen lyfter således upp ringen på ungefär 4.3 sekunder.