Lägesenergi och potentiell energi

Lägesenergi är en potentiell energi, vilket också är ett namn som ofta används. Ett föremål får en potentiell energi, lägesenergi när det höjs upp ovanför nollnivån. Exempelvis bygger en människa upp en lägesenergi när denne klättrar upp för ett hopptorn, lägesenergin kan sedan omvandlas till rörelseenergi i hoppet på väg ner.

Om vi bär upp en sten till första våningen har den fått en lägesenergi i förhållande till marken, bär vi upp den till andra våningen har den fått ännu mer lägesenergi.

Formel för lägesenergi

Formeln för lägesenergi skrivs som

\[ W_p = mgh\]

där \(m\) är massan, \(g\) tyngdaccelerationen och \(h\) höjden över nollnivån. Formeln kan härledas från fysikaliskt arbete, där kraften ersätts med tyngdkraften och sträckan med höjden. Enheten för potentiell energi, lägesenergi och all annan energi är Joule.

Exempel på lägesenergi

Pelle har massan 84.5 kg och står i badhuset. Först tänker han hoppa från 7ans plattform och sedan från 10an. Hur stor är Pelles lägesenergi vid varje avsats?

Vi använder formeln rakt av och sätter in, vi börjar med lägesenergin från 7 meter. För jordens tyngdacceleration nyttjar vi \(9.8~\text{m}/\text{s}^2\).

\[ W_p = 84.5 \cdot 9.8 \cdot 7 = 5796.7~\text{J} \approx 6000~\text{J}\]

På samma sätt gör vi för höjden 10 meter, in i formeln och slå på en miniräknare alternativt bra handräknat.

\[ W_p = 84.5 \cdot 9.8 \cdot 10 = 8281~\text{J} \approx 8000~\text{J}\]

Avrundningarna görs eftersom vi inte har några fler värdesiffror för höjden på plattformarna för hopptornet.

Lägesenergi beror inte på vägen upp

Lägesenergi är inte beroende på vägen upp till höjden. Du får således samma lägesenergi om du åker hiss till högsta våningen eller tar trapporna dit, även om det kanske är en längre och jobbigare väg att ta trapporna än hissen.

Vad menar vi med nollnivå?

När vi använder ordet nollnivå i samband med lägesenergi menar vi den nivå där energin är noll. Det är en nivå som egentligen är valfri för dig som räknar, rent fysikaliskt finns det ingen skillnad så länge alltid samma används. Det finns däremot mer eller mindre klyftiga nivåer att sätta. Den allra vanligaste och oftast mest användbara är att använda jordens yta som nollnivå, är ett föremål över jordytan har det en positiv lägesenergi, och är det under jordytan har det en negativ lägesenergi i förhållande till nollnivån.

Lägesenergi till rörelseenergi med olika nollnivåer

Renströmsgruvan i Västerbotten är en av Sveriges djupaste gruvor med verksamhet 1500 meter under markytan. En sten ramlar ur en skopa 2.5 meter över markytan i en gruvgång. Med vilken hastighet träffar stenen gruvgången?

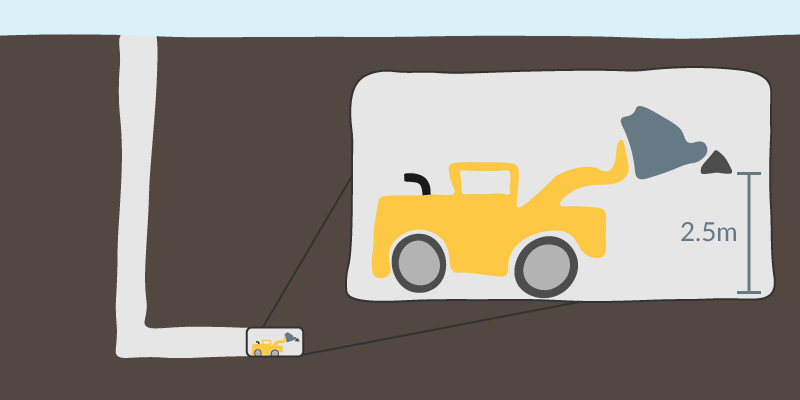
Istället för att sätta jordskorpan till nollnivå sätter vi gruvgångens mark som nollnivå, eftersom det är där stenen faller till marken och således området som är intressant för oss. Själva uppgiften löser vi med hjälp av energiprincipen, lägesenergin stenen har från att ha blivit upplyft i skopan ska omvandlas till rörelseenergi på vägen ner. Vi börjar med att sätta upp ekvationen för lägesenergi.

\[ W_p = mgh\]

All denna energi ska omvandlas till rörelseenergi på vägen ner. Vi använder indexet \(k\) då rörelseenergi är en synonym till kinetisk energi.

\[ W_k = \frac{mv^2}{2}\]

Dessa två sätter vi nu lika med varandra.

\[ W_p = W_k\]

Sätt in respektive uttryck och sedan är målet att lösa för hastigheten \(v\).

\[ mgh = \frac{mv^2}{2}.\]

Vi kan stryka massan ur båda leden.

\[ gh = \frac{v^2}{2}\]

Multiplicera med \(2\) och dra roten ur båda leden för att erhålla hastigheten \(v\).

\[ v = \sqrt{2gh}\]

Om vi nu sätter in de numeriska värdena,

\[ v = \sqrt{2 \cdot 9.8 \cdot 2.5 } = 7~\text{m/s.}\]

Stenen träffar således gruvgången med en hastighet av 7 m/s. Samma princip kan användas för att räkna ut hur fort Pelle slår i vattenytan när han hoppar från hopptornet ovan.