Rörelsemängd i två dimensioner

Hej! Idag ska vi titta närmare på rörelsemängd i två dimensioner. Detta kommer vi göra genom att komposantuppdela rörelsemängden i en horisontal och en vertikal vektor.

I figur 1 nedan har vi ritat ut två bilar som möter varandra i en korsning på en isbana. Således tar vi inte hänsyn till friktion, luftmotstånd eller annat. Vi antar att vi känner till de båda bilarnas massor och hastighet.

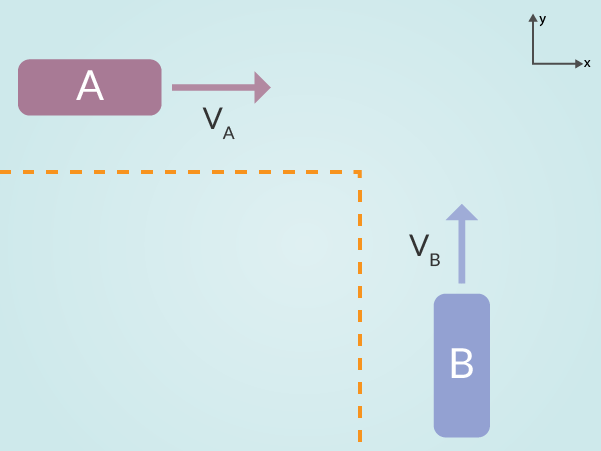
Då ingen av förarna har vett nog att bromsa kolliderar de båda ihop till en enda stor klump som i figur 2. Vilken hastighet och vilken riktning har klumpen med bilarna?

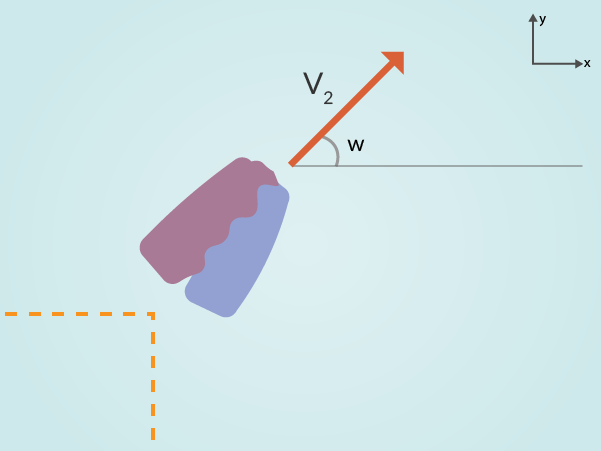
En liten ledning finns i figur 2. Vi kommer nyttja lagen om rörelsemängdens bevarande och det faktum att rörelsemängd är en vektor. Då kan vi dela upp den i horisontalled och vertikalled med hjälp av vinkeln som vi kallar för \(w\). Den här vinkeln kommer dessutom hjälpa till med att svara på frågan om vilken riktning klumpen har efteråt.

Vi börjar med rörelsemängden för respektive riktning. Vi använder att rörelsemängden före är lika stor som rörelsemängden efteråt.

Horisontell rörelsemängd (x-axeln)

\[ m_A v_A = (m_A + m_B)v_2\cos(w)\]

Här har vi komposantuppdelat rörelsemängden med hjälp av trigonometri. Mer information om hur det går till finns under dela upp en kraft.

Vertikal rörelsemängd (y-axeln)

\[ m_B v_B = (m_A + m_B)v_2\sin(w)\]

Givetvis har vi använt trigonometri för att titta på rörelsemängden som rör sig vertikalt här också.

Ekvationssystem med två obekanta

Vi sammanfattar ekvationssystemet som ska lösas

\[ \begin{cases} m_A v_A = (m_A + m_B)v_2\cos(w) \\ m_B v_B = (m_A + m_B)v_2\sin(w) \end{cases}\]

Vi har ett icke-linjärt ekvationssystem med 2 variabler. Det finns flera olika sätt att lösa detta. Vi kommer visa två metoder som kan vara ett utgångläge. Känner man till den ena är det lätt att räkna den andra genom att bara substituera in den andra.

Vinkeln med hjälp av ledvis division

Tanken här är att vi dividerar den undre ekvationen med den övre. Detta får vi göra, eftersom de är lika måste kvoten av vänsterleden och högerleden också vara lika.

\[ \frac{m_B v_B}{m_A v_A } = \frac{(m_A + m_B)v_2\sin(w)}{(m_A + m_B)v_2\cos(w)}\]

Nu kan vi stryka \((m_A + m_B)\) och \(v_2\). Då återstår endast vinkeln \(w\) att lösa ut.

\[ \frac{m_B v_B}{m_A v_A } = \frac{\sin(w)}{\cos(w)}\]

Från trigonometrin hämtar vi att tangens är lika med kvoten mellan sinus och cosinus.

\[ \frac{\sin(w)}{\cos(w)} =\tan(w)\]

Ekvationen skrivs med hjälp av tangens istället.

\[ \frac{m_B v_B}{m_A v_A } =\tan(w)\]

Vinkeln kan lösas ut med hjälp av inversen till tangens.

\[ w = \arctan\Bigg(\frac{m_B v_B}{m_A v_A }\Bigg)\]

Givetvis är vi bara intresserade av vinkeln som ligger mellan 0 och 90 grader. Nu kan vi substituera in vinkeln i någon av ekvationerna och lösa ut \(v_2\), alternativt använda metoden nedan.

Hastigheten efter med hjälp av ledvis addition

Nu kvadrerar vi båda leden och sedan faktoriserar vi. De trigonometriska termerna kommer försvinna tack vare trigonometriska ettan.

\[ \begin{cases} (m_A v_A)^2 = [(m_A + m_B)v_2\cos(w)]^2 \\ (m_B v_B)^2 = [(m_A + m_B)v_2\sin(w)]^2 \end{cases}\]

Med hjälp av exponentlagarna får vi flytta in potensen på respektive faktor.

\[ \begin{cases} (m_A v_A)^2 = (m_A + m_B)^2{v_2}^2\cos^2(w) \\ (m_B v_B)^2 = (m_A + m_B)^2{v_2}^2\sin^2(w) \end{cases}\]

Termerna adderas ledvis. Detta får vi också göra eftersom likhet råder.

\[ (m_A v_A)^2 +(m_B v_B)^2 =  (m_A + m_B)^2{v_2}^2\sin^2(w) +(m_A + m_B)^2{v_2}^2\cos^2(w)\]

Bryt ut och faktorisera i högerledet.

\[ (m_A v_A)^2 +(m_B v_B)^2 =  (m_A + m_B)^2{v_2}^2\Big(\sin^2(w) +\cos^2(w)\Big)\]

Vi minns den trigonometriska ettan

\[ \sin^2(w) +\cos^2(w) = 1\]

Sätt in detta i ekvationen,

\[ (m_A v_A)^2 + (m_B v_B)^2 = (m_A + m_B)^2{v_2}^2 \cdot 1\]

Division med \((m_A + m_B)^2\) och hastigheten står ensam.

\[ \frac{(m_A v_A)^2 +(m_B v_B)^2}{(m_A + m_B)^2} = {v_2}^2\]

Vi drar roten ur båda leden.

\[ v_2 = \sqrt{\frac{(m_A v_A)^2 +(m_B v_B)^2}{(m_A + m_B)^2}}\]

Då var vi färdiga med två formler. Nedan provar vi ett numeriskt exempel.

Exempel på rörelsemängd i två dimensioner

Låt oss säga att bil A har en massa, \(m_A = 1520~\text{kg}\) och en hastighet på \(v_A = 4.53~\text{m/s}\), medan bil B har en massa på \(m_B = 1670~\text{kg}\) och en hastighet på \(v_B = 7.29~\text{m/s}\). Hur stor är hastigheten efter kollisionen och vilken vinkel mot horisontalplanet har klumpen?

Vi börjar med vinkeln,

\[ w = \arctan\Bigg(\frac{1670\cdot7.29}{1520\cdot4.53 }\Bigg) = 1.056...~\text{rad} \approx 60.5 ^{\circ}.\]

Detta känns rimligt, bilen B har större massa och högre hastighet, då borde logiskt sett vinkeln bli större. Nu beräknar vi hastigheten efter kollisionen.

\[ v_2 = \sqrt{\frac{(1520\cdot4.53)^2 +(1670\cdot7.29)^2}{(1520 +1670)^2}} \approx 4.38~\text{m/s.}\]

Sammanfattningsvis kan vi säga bilklumpen efter kollisionen har hastighet på 4.38 m/s med vinkeln 60.5° från horisontalplanet.