Lägga ihop krafter
Det är viktigt att kunna lägga ihop krafter i fysiken, exempelvis vid beräkningar där Newtons andra lag används. I Denna genomgång tittar vi på hur man kan addera krafter.
En kraft är en vektor, vilket betyder att den har en storlek och en riktning. Detta innebär att du kan använda genomgången nedan för att lägga ihop exempelvis hastighet och acceleration, som också är vektorer.
Vi använder oss av ett rutat papper, där vi exempelvis kan sätta att en ruta är 1 Newton, men det själva konceptet som är viktigt.
Krafter som ligger på rad
Krafter som ligger på rad kan enkelt summeras som de gjort i figur 1.
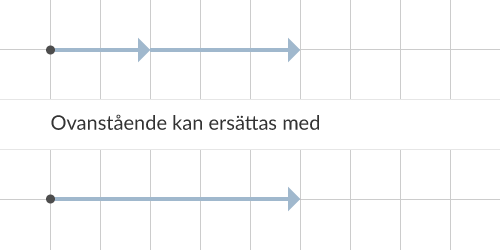
Om krafterna inte är motriktade kan de enkelt subtraheras mot varandra som i figur 2.

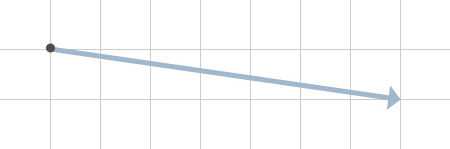
Krafterna behöver inte ens ligga fint i rutnätet, utan bara de är på samma "linje". Ett exempel på detta finns i figur 3.
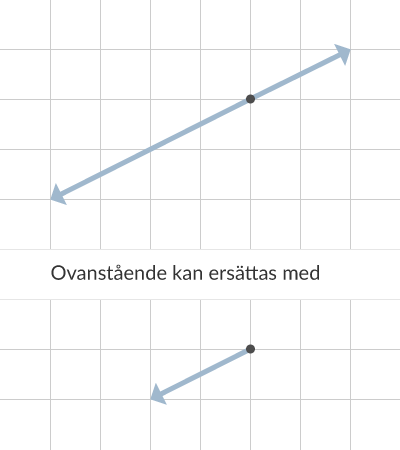
Två vinkelräta krafter
Det är vanligt att man i fysiken har två krafter som är vinkelräta mot varandra. Detta eftersom att man ofta delar upp situationen i en vertikal situation och en horisontal situation, och när dessa sedan ska slås ihop ser det ut på följande vis.
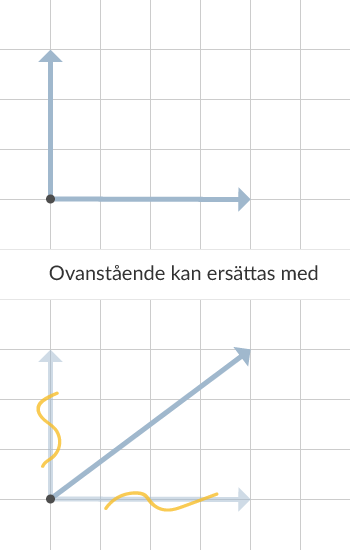
De gula ormarna sätter vi ut för att hålla koll på vilka krafter som använts och bildat den resulterande kraften. Inget måste men underlättar mycket om det är många krafter. Det är därför rekommenderat att använda sig av dessa.
Längden av den resulterande kraften kan enkelt beräknas med hjälp av Pythagoras sats.
Två godtyckliga krafter
Ibland ligger inte krafterna på en linje eller är vinkelräta. Då kan det exempelvis se ut som i figur 5. Det finns tillvägagångssätt för att hitta den resulterande kraften även här.
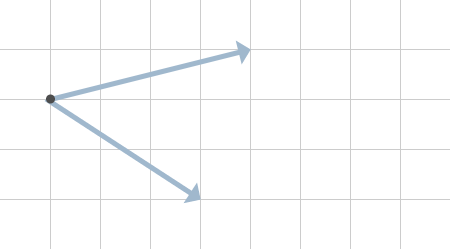
Det vi gör nu är att rita ut ett par stödlinjer. Detta gör vi genom att ta vardera kraft och flytta till spetsen på den andra kraften som visas i figur 6. Dessa linjer är inga krafter utan funderar enbart som stöd för att vi ska kunna rita ut den resulterande kraften.
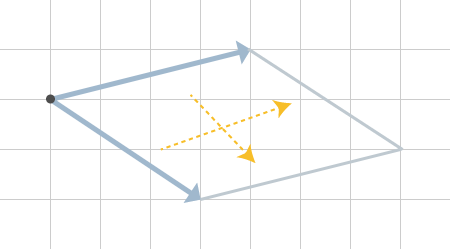
Nu drar vi en linje från vår ursprungliga punkt, tvärs över fyrhörningen till den andra spetsen. Denna linje är den resulterande kraften som i figur 7.
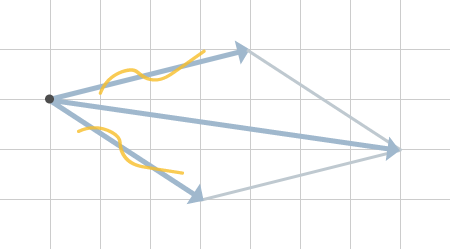
Vi kan nu sudda ut de två gamla krafterna, samt våra gula markeringar och ensamt rita ut kraften. Detta har gjorts i figur 8.
Tre eller fler krafter
När vi vill addera tre krafter eller fler är det egentligen inte svårare än att addera två krafter. Det vi gör är att vi adderar två krafter åt gången tills vi endast har en resulterande kvar. Låt oss plocka fram den resulterande kraften till figur 9.
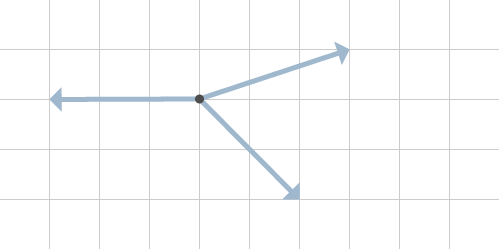
De två krafterna till höger om punkten väljs för att hitta deras kraftresultant. Detta görs genom att rita ut stödlinjer och dra en linje genom fyrhörningen. Figur 10 illustrerar detta.
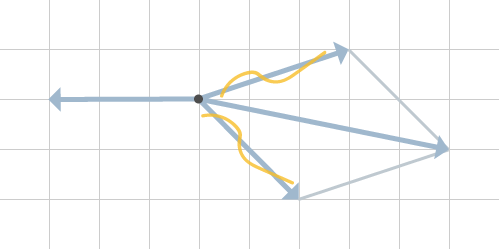
Vi är tillbaka på en situation med 2 krafter som figur 11 visar.
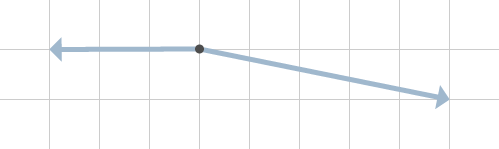
Precis som förut ritar vi ut stödlinjer och drar ut den resulterande kraften. Detta visas i figur 12.
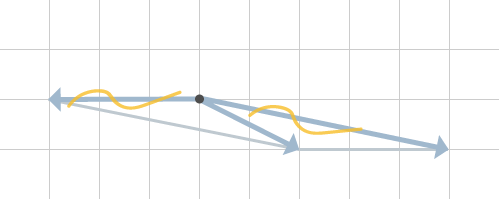
Nu är vi framme vid den resulterande kraften, vilket vi ensamt kan rita ut på så sätt som i figur 13.
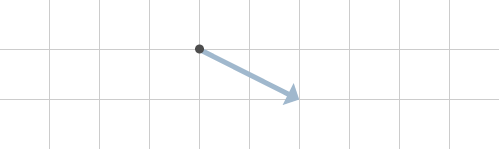
Dela upp och sedan lägga ihop
Ibland kan det vara lättare att först dela upp krafterna i komposanter för y och x-axeln och därefter räkna ut den resulterande kraften. Du kan läsa mer om hur man delar upp krafter under "dela upp krafter".