Hastighet-tid-graf för en bil på en parkeringsplats

Hej! Vi har tidigare tittat på hastighet-tid till kraft-tid uppgift, och en sträcka-tid-graf, nu fortsätter vi med en hastighet-tid-graf till.

I figur 1 finns ett diagram över hastigheten för en bil som rullar in på en parkeringsplats.

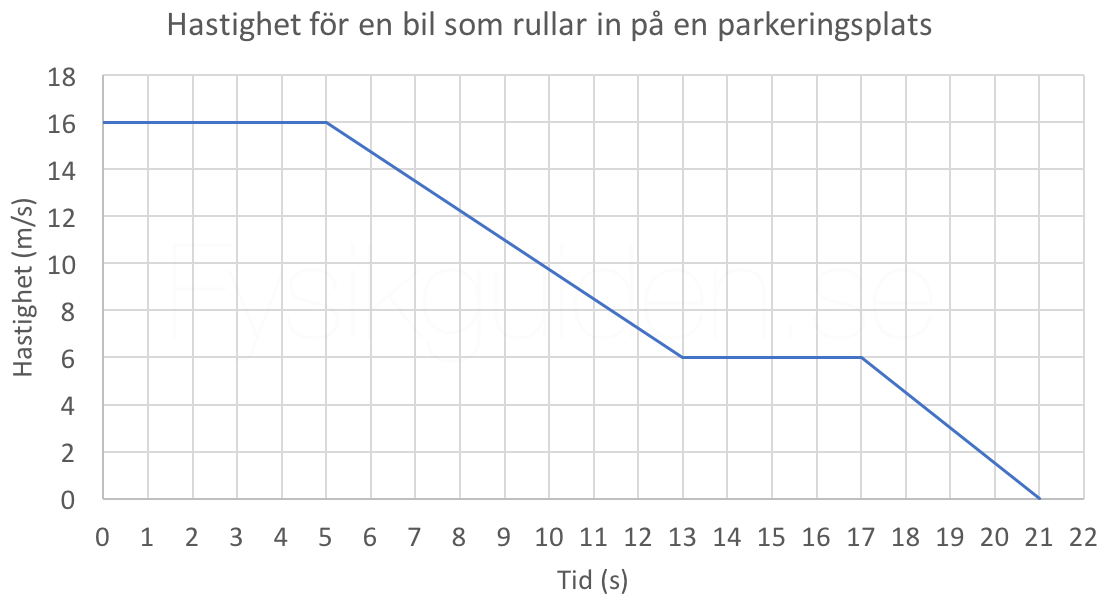
Till den här grafen har vi fyra stycken frågor vi vill besvara.

• Hur fort kör bilen vid tidpunkten 9 sekunder?
• Vid vilken tidpunkt är hastigheten 4 m/s?
• Vad är accelerationen vid tidpunkten 7 sekunder?
• Hur långt har bilen kört totalt från när den rullar in på parkeringsplatsen tills den är parkerad? Vi tar frågorna i uppskriven ordning.

Hur fort kör bilen vid tiden 9 sekunder?

När vi vill ta reda på hur fort bilen kör vid en given tidpunkt går vi från tidsaxeln upp till grafen, och sedan rätt in på y-axeln där hastigheten kan avläsas, det är illustrerat i figur 2.

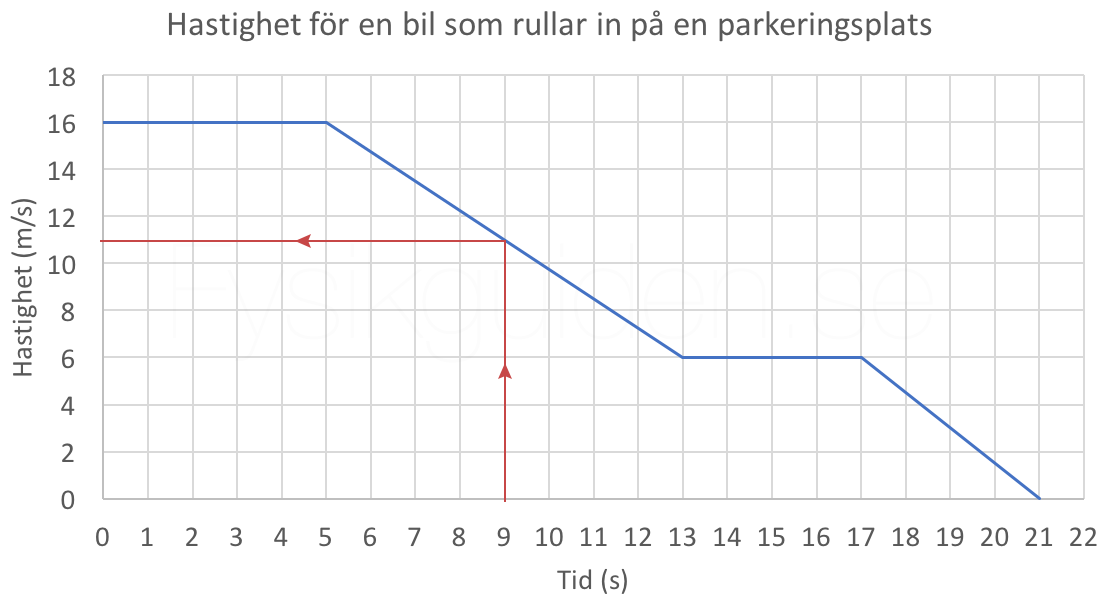
Vi kan läsa av 11 m/s på y-axeln. Vi går vidare till nästa fråga där vi går åt andra hållet.

Vid vilken tidpunkt är hastigheten 4 m/s?

När vi vill ta reda på vid vilken tidpunkt hastigheten är ett speciellt värde går vi åt andra hållet. Vi går från y-axeln rätt in tills vi träffar grafen och sedan rätt ner mot tidsaxeln. I figur 3 har vi illustrerat detta med pilarna.

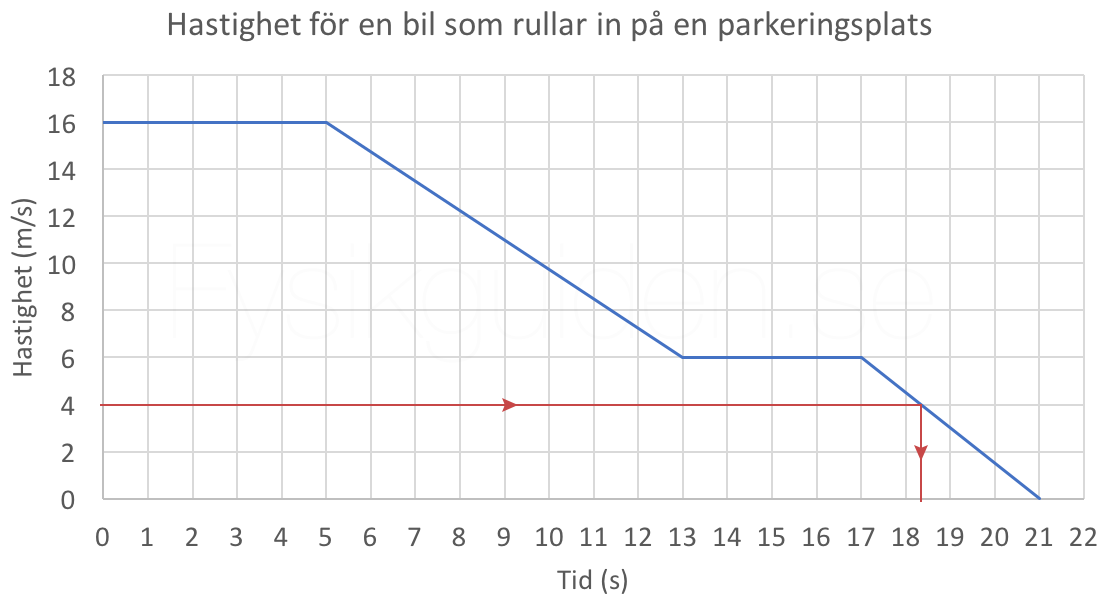
Här blir avläsningen lite svårare, men om vi svarar runt 18.3 sekunder bör vi träffa någorlunda rätt. Det exakta svaret är 18.333..., så om vi svarar där omkring är vi nöjda. Under 18 eller över 19 är däremot uppenbart fel.

Vad är accelerationen vid tiden 7 sekunder?

Accelerationen kan vi räkna ut genom att vi vet att det är lutningen i en hastighet-tid-graf. Vid 7 sekunder lutar grafen lika mycket som hela den rödmarkerade delsträckan, således kan vi räkna ut lutningen mellan de punkterna för dessa är enkla att se värden på i grafen.

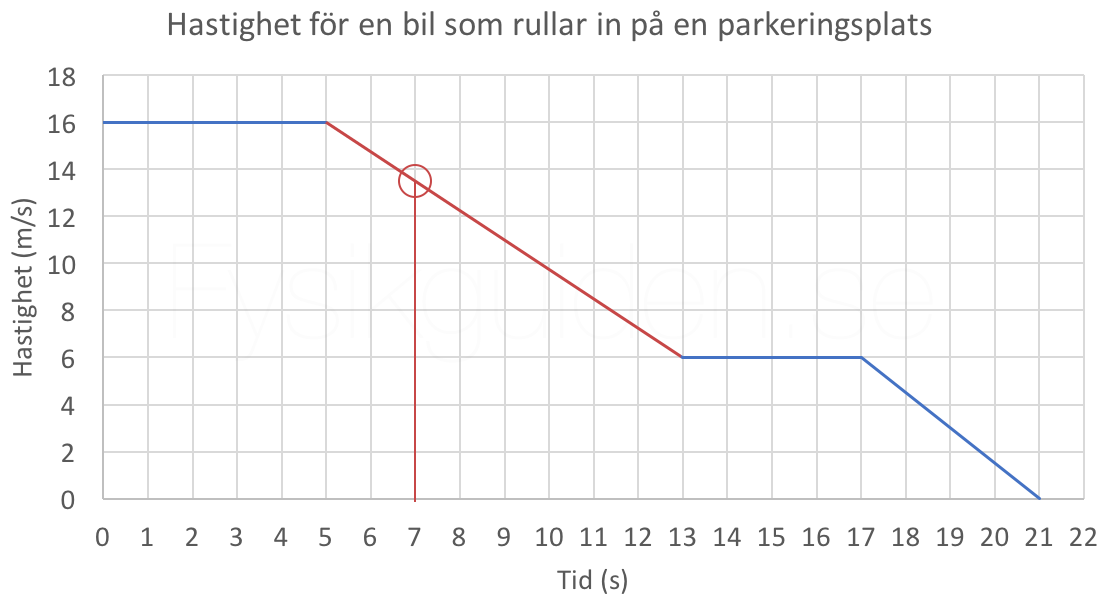
Vi sätter upp formeln för acceleration,

\[ a = \frac{\Delta v}{\Delta t}.\]

Vi väljer tiden mellan 5 och 13 sekunder.

\[ a = \frac{6-16}{13-5}\]

Vilket ger en acceleration på

\[ a =-1.25~\text{m}/\text{s}^2.\]

Det negativa svaret är rimligt, då grafen lutar nedåt i det sökta intervallet.

Hur långt har bilen kört totalt?

För att beräkna hur långt bilen har kört använder vi att arean under en hastighet-tid-graf är sträckan. Vi har tur för vår graf är skarp och kan delas in i kända geometriska former.

Vi räknar ut sträckan genom att addera \(A\), \(B\), \(C\) och \(D\).

\[ s = A + B + C + D\]

Rektangels area är basen multiplicerad med höjden, triangelns area är basen multiplicerad med höjden dividerat med 2. Den totala sträckan kan då skrivas som

\[ s = 5 \cdot 16 + (17-5)\cdot 6 + \frac{(13-5)\cdot(16-6)}{2} + \frac{(21-17)\cdot 6}{2}.\]

Slås detta på en räknedosa,

\[ s = 204~\text{m.}\]

Då vet vi att från att bilen rullat in på parkeringsplatsen tills den är parkerad har den rullat 204 meter.