Oelastisk stöt

Hej! Idag ska vi titta på ett exempel på en oelastisk stöt där en bil stöter in i en annan. Tidigare kunskaper om rörelseenergi, rörelsemängd och stötar kan vara bra.

Metod för att lösa uppgiften

Först ritar vi en bild över situationen. Därefter ställer vi upp lagen om rörelsemängdens bevarande och beräknar där hur stor bil B's hastighet är efter stöten. Med hjälp av att vi vet att rörelseenergin är större före stöten visar vi att stöten är oelastisk.

Utförande och uppställning

En bild av problemet underlättar räknandet och uppställningen av problemet. Nedan i figur 1 visas hur det ser ut före stöten.

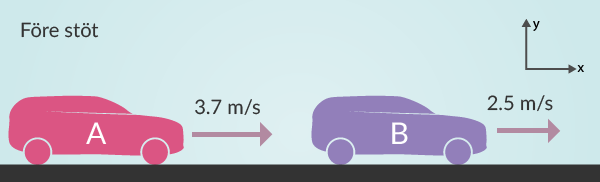
I figur 2 nedan har vi illustrerat hur det ser ut efter stöten. I båda figurerna har vi markerat positiv riktning uppe i högra hörnet. Allt som rör sig åt höger är positivt och allt som rör sig åt vänster är negativt. Detta spelar ingen roll i just det här fallet då allt är på väg till höger.

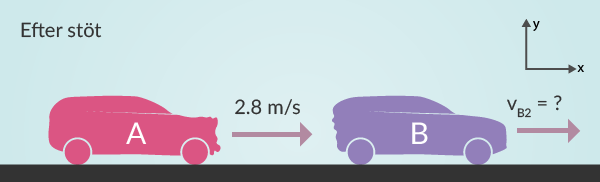
Inledningsvis ställer vi upp lagen om rörelsemängdens bevarande.

$$\vec{\boldsymbol{p}}_{\text{före}} =\vec{\boldsymbol{p}}_{\text{efter}}$$

Båda bilarna är båda på väg åt höger i båda fallen, höger har vi definierat som positiv riktning uppe i hörnet. Det ger följande rörelsemängd, där $m_A$ och $m_B$ är massorna för respektive bil. Varje bils hastighet indikeras med bokstav i index. En $1$ efter bokstaven talar om att det är före stöten, medan $2$ är efter stöten.

$$m_A v_{A1} + m_Bv_{B1} =  m_Av_{A2} +m_Bv_{B2}$$

Ur detta vill vi lösa ut $v_{B2}$. Först subtraheras $m_av_{A2}$ från båda sidorna.

$$m_A v_{A1} + m_Bv_{B1} -m_Av_{A2} = m_Bv_{B2}$$

Bryt ut massan $m_A$ för att snygga upp det lite.

$$m_A(v_{A1} -v_{A2}) + m_Bv_{B1} = m_Bv_{B2}$$

Division med $m_B$ och vårt uttryck är färdigt.

$$\frac{m_A(v_{A1} -v_{A2}) + m_Bv_{B1} }{m_B} = v_{B2}$$

Vi beräknar ett numeriskt värde genom att sätta in våra siffror.

$$v_{B2} = \frac{1250\cdot(3.7 -2.8) + 1450\cdot2.5}{1450}$$

Detta slaget på en räknedosa ger

$$v_{B2} = 3.27586... \approx 3.3~m/s.$$

Nu ska vi visa att stöten är oelastisk. Detta görs genom att följande måste vara sant.

$$\text{Rörelseenergi före} > \text{Rörelseenergi efter}$$

Vi ställer upp respektive rörelseenergi och kikar om olikheten är uppfylld.

$$\frac{m_Av_{A1}^2}{2} + \frac{m_Bv_{B1}^2}{2} >  \frac{m_Av_{A2}^2}{2} +\frac{m_Bv_{B2}^2}{2}$$

Sätt in numeriskt,

$$\frac{1250\cdot3.7^2}{2} + \frac{1450\cdot2.5^2}{2} > \frac{1250\cdot2.8^2}{2} + \frac{1450\cdot3.2786^2}{2}.$$

Utvärdera med hjälp av en räknedosa.

$$13087.5 ~\text{J} > 12680.17...~\text{J}.$$

Olikheten stämmer, alltså är stöten oelastisk.

Svar: Bil Bs hastighet efter stöten är 3.3 m/s, stöten är oelastisk då rörelseenergin är mindre efter än före.