Centripetalacceleration
En bil som kör in i en kurva ändrar sin riktning. Det som ger upphov till denna ändring kallas centripetalacceleration. I figur 1 visas en bil eller något annan som åker in i en cirkulär bana med en hastighet.
Formel för centripetalacceleration
\[ a_c = \frac{v^2}{r}\]
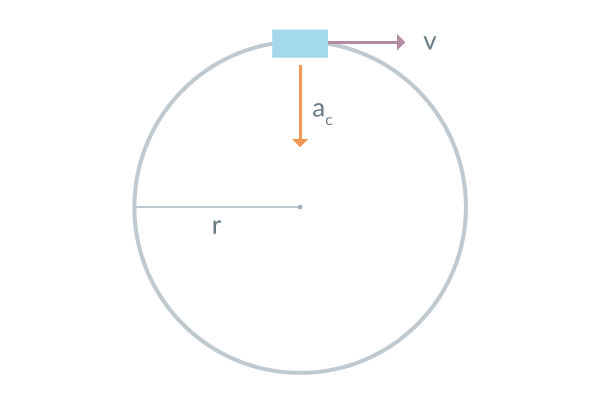
Där hastigheten är vinkelrät mot radien. Härledning av formeln kan göras genom likformighet i figur eller med hjälp av dimensionsanalys.
Fler formler finns längre ner.
När centripetalaccelerationen slutar verka
Elvira har börjat med friidotten släggkastning. Hon står roterar ett klot i enlighet med figur 1. Vi ritar ut centripetalaccelerationen och hastigheten.
I en given tidpunkt så släpper Elvira släggan och då fortsätter släggan med samma riktning som hastigheten. Riktningen som klotet fortsätter på är tangenten på cirkeln hon roterat i. Detta illustrerar vi i figur 2.
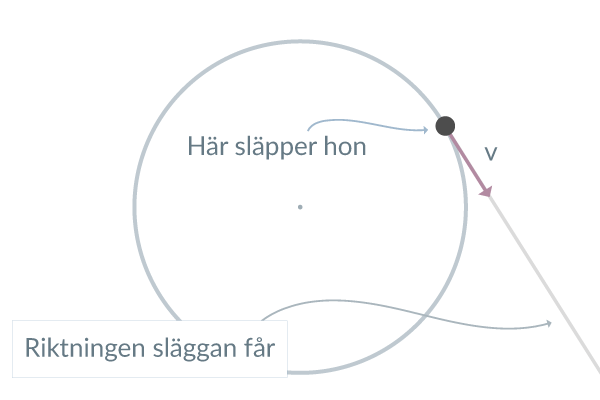
Detta låter ju rimligt, för om släggan skulle fortsatt i en cirkel skulle friidrottsgrenen bli tämligen svår att utöva.
Exempel på centripetalacceleration
En cyklist cyklar med en hastighet av 8 m/s och cyklar in i en perfekt cirkulär kurva med radien 16 meter. Hur stor centripetalaccelerationen verkar på cyklisten?
\[ a_c = \frac{v^2}{r}\]
Då alla värden vi har är i samma enhet kan vi enkelt beräkna centripetalaccelerationen.
\[ a_c = \frac{8^2}{16} = 4~m/s^2.\]
Cyklisten har en centripetalacceleration på 4 m/s2. Detta kommer göra att cyklisten ändrar riktning, med andra ord svänger.
Andra formler för centripetalacceleration
Det finns ett par formler till som kan vara användbara. Dessa utgår ifrån omloppstid \(T\), frekvens \(f\) och vinkelhastighet \(\omega\) istället för hastighet.
\[ a_c=\frac{4{\pi}^2r}{T^2}\]
\[ a_c=4{\pi}^2{f}^2r\]
\[ a_c={{\omega}^2}r\]
Exempel på centripetalacceleration med omloppstid
Hanna snurrar ett 60 cm långt nyckelband med en nyckel längst ut flera varv. Då det är svårt att mäta precis ett varv så mäter hennes kompis upp att det tar 15 sekunder för henne att snurra nyckelbandet 30 varv. Hur stor centripetalacceleration verkar på nyckeln?
Det första vi kan göra är att konvertera enheten till meter.
\[ 60 ~\text{cm}= 0.60 ~\text{m}.\]
Vi kan beräkna omloppstiden genom att ta tiden dividerat med antal varv.
\[ T = \frac{\text{tid}}{\text{antal varv}} = \frac{15}{30} = 0.5~\text{s.}\]
Ett varv tar således 0.50 sekunder att genomföra.
Vi kan använda den första formeln ovan för att beräkna centripetalaccelerationen.
\[ a_c=\frac{4{\pi}^2r}{T^2} = \frac{4{\pi}^2 \cdot 0.60}{0.50^2} \approx95~m/s^2.\]
Centripetalkraft
Centripetalacceleration blir ofta lite mer spännande när det sätts ihop med en massa och bildar den resulterande kraften. Läs mer om detta under centripetalkraft.