Hookes lag och kraften i en fjäder

Hookes lag säger att kraften i en fjäder kan skrivas som

\[ F = kx\]

Där \(F\) är kraften, \(k\) är fjäderkonstanten, och \(x\) är positionen från jämviktsläget.

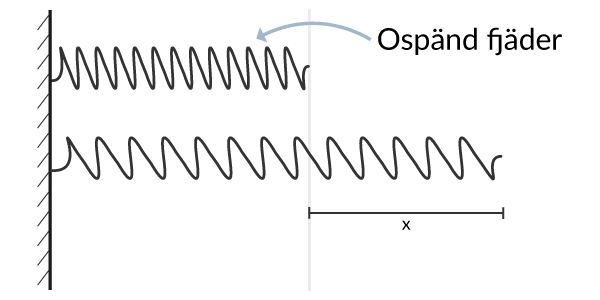
Fjäderkonstanten k

Varje fjäder har en fjäderkonstant. Fjäderkonstanten har enheten \(\text{N/m}\). Desto större fjäderkonstant, desto mer kraft behövs för att dra ut fjädern.

Detta gäller inom ett visst intervall, om vi drar ut fjädern alldeles för långt går den sönder och återfår inte sin form, samma sak om vi trycker ihop den alldeles för hårt.

Exempel på Hookes lag

Pelle har en fjäder med fjäderkonstanten 61 N/m och drar ut den 0.82 m från sitt jämviktsläge. Hur stor kraft behöver Pelle dra med?

Vi nyttjar Hookes lag för kraften i en fjäder.

\[ F = 61\cdot0.82 \approx 50~\text{N.}\]

Således behöver Pelle dra med 50 Newton för att fjädern ska sträckas ut 0.82 m.

Beräkna utdragen sträcka

En massa på 2.16 kg hänger stilla i taket med hjälp av en fjäder som har en fjäderkonstant på 51.9 N/m. Hur långt är fjädern utdragen? Vi skissar en bild över situationen.

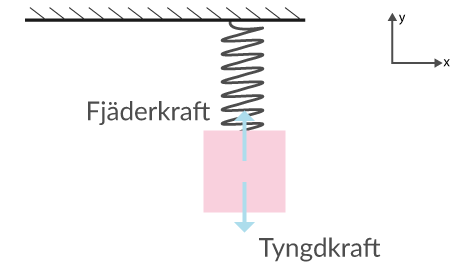
Vi använder Newtons lagar, då vi vet att massan står stilla är summan av krafterna som verkar på den noll.

\[ \sum F = 0\]

De krafter som finns är tyngdkraften och fjäderkraften. Om vi sätter positiv riktning uppåt kan det skrivas som

\[ -mg + kx = 0.\]

Det låter rimligt, om tyngdkraften är precis samma som fjäderkraften är de i jämvikt.

\[ kx = mg\]

Dividera med fjäderkonstanten och den utdragna sträckan kan beräknas numeriskt.

\[ x = \frac{mg}{k}\]

Ett numeriskt värde,

\[ x = \frac{2.16\cdot9.82}{51.9} \approx 0.409~\text{m.}\]

Om vi nu skulle dra ner massan lite till och släppa den kommer massan att börja svänga.

Fjäderns svängingstid

Svängningstiden för en period för en fjäder kan skrivas som

\[ T = 2\pi \sqrt{\frac{m}{k}}\]

Mer om det finns under sidan fjäderns svängningstid.

Ibland finns ett minustecken

Ibland skrivs Hookes lag som

\[ F = -kx.\]

Detta beror på om man ser på fjäderkraften som reaktionskraft eller inte. Det är inget vi behöver oroa oss över utan våra uppgifter kommer bli korrekt ändå.