Dela upp en kraft och komposantuppdela en vektor
I denna genomgång ska vi titta på hur man kan komposantuppdela en kraft. Då kraft är en vektor fungerar det på samma sätt om du vill komposantuppdela exempelvis hastighet, acceleration eller rörelsemängd. Vi använder exempelvis följande metod i kaströrelsen.
Oftast ser det ut som i figur 1, en kraft med en vinkel mot horisontalplanet.
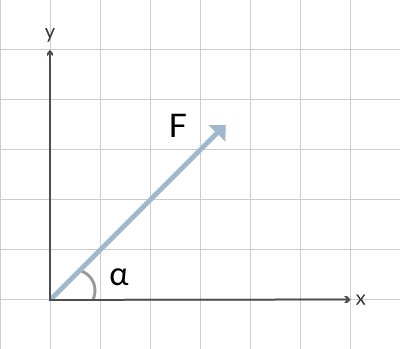
Med hjälp av trigonometri kan vi hitta den vertikala och horisontala komposanten. Dessa återfinns i figur 2.
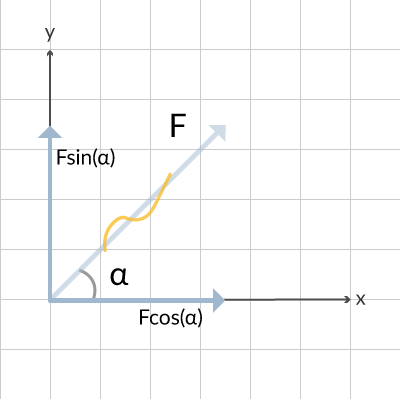
Dessa skrivs ofta om med hjälp av ett litet index för respektive axel. Då ser det ut på följande vis
\[ F_x = F\cos{\alpha}\]
\[ F_y = F\sin{\alpha}\]
Detta kan exempelvis vara ett sätt att städa upp ens beräkningar med och göra dessa mer lättöverskådliga.
Exempel på kraftuppdelning
Vi ska nu titta på ett exempel. En kraft på 584 Newton har en vinkel på 31° mellan kraften och horisontalplanet som i figur 3. Hur stora är krafterna i y respektive x-led?
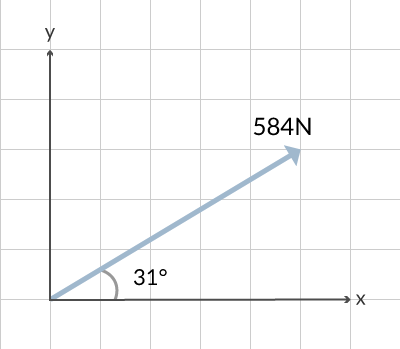
Vi tar formeln eller bilden till hjälp och beräknar kraftkomposanterna.
\[ F_x = F\cos{\alpha} = 584\cdot\cos(31 ^{\circ}) \approx 501~\text{N.}\]
\[ F_y = F\sin{\alpha} = 584\cdot\sin(31 ^{\circ}) \approx 301~\text{N.}\]
Vi kan nu ersätta kraften med en kraft i x-led och en kraft i y-led som är vinkelräta mot varandra. Det visar vi i figur 4.
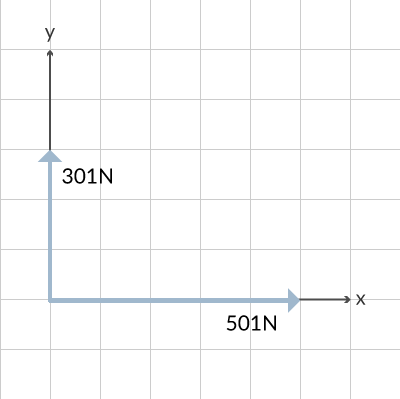
Då de flesta värden på sinus och cosinus är långa decimaltal, så blir komposanterna också decimaltal. Detta gör att vi får avrunda något.