Sammanfattning om grafer
I denna genomgång tittar vi närmare på vad som gäller för olika typer av diagram. Vi kikar närmare på vad vi kan utläsa i grafer som beskriver sträcka, hastighet eller acceleration som funktion av tiden.
Sträcka-tid graf
En sträcka-tid graf förkortas ofta till st-graf eller st-diagram. Ett exempel på en st-graf är figur 1.
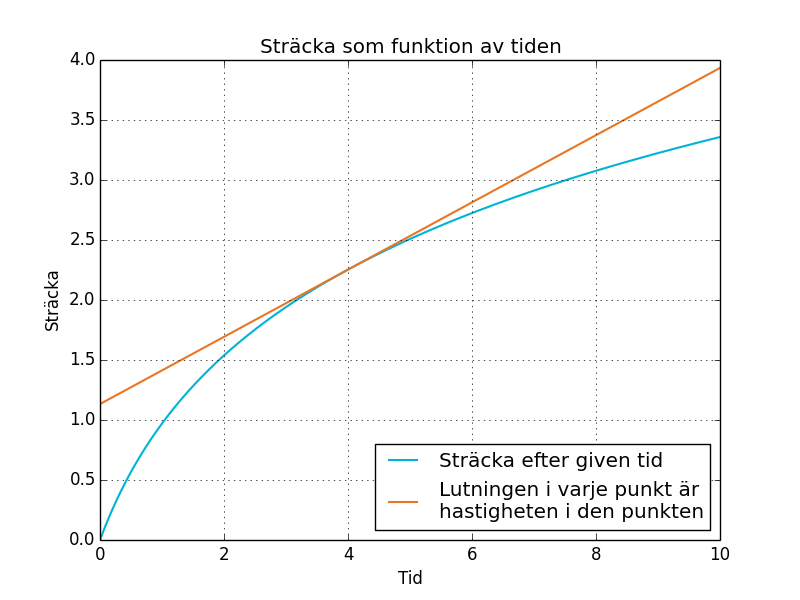
Lutningen på kurvan kan vi få ut någorlunda approximativt genom att beräkna riktningskoefficient mellan två punkter som är väldigt nära varandra. Om du behärskar derivering är det givetvis ett behändigt hjälpmedel för att beräkna lutningen exakt.
Ett exempel på när en sträcka-tid-graf finns på knappen under, där lär vi oss hur vi kan se sträcka efter en viss tid men även hur man räknar ut medelhastighet i ett sådant diagram.
Hastighet-tid graf
Ett hastighet-tids diagram förkortas ofta vt-graf eller vt-diagram. Ett exempel på ett sådant är figur 2.
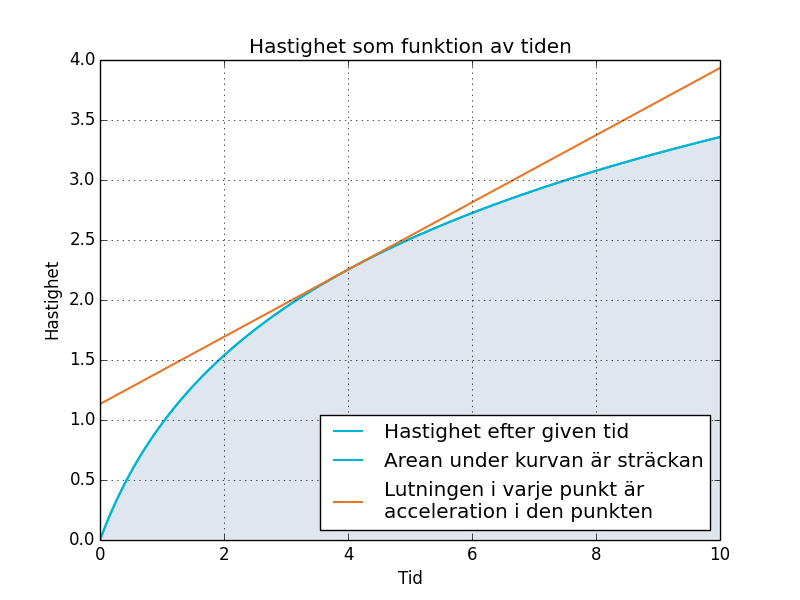
Lutningen i en vt-graf är accelerationen och kan precis som för en st-graf fås genom riktningskoefficient mellan två nära valda punkter eller genom derivering.
Arean under kurvan är den totala sträckan föremålet färdats. Om det är enkla former, typ kvadrater och trianglar kan arean beräknas på vanligt sätt.
Ett annat sätt är med hjälp av matematisk integration vilket introduceras i matematik 3 på gymnasiet.
Ett exempel på när vi nyttjar hastighet-tid-grafen för att ta reda på både hastighet vid given tidpunkt, sträckan efter en tid och accelerationen vid en viss tidpunkt finns på knappen här under.
Acceleration-tid graf
Acceleration-tids diagram förkortas ofta at-diagram eller at-graf. Ett exempel på ett sådant är figur 3.
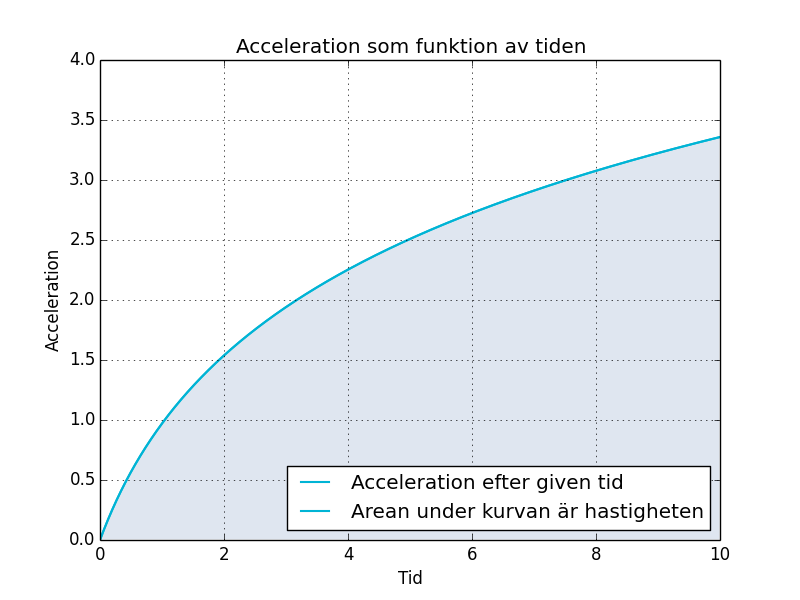
Arean under kurvan i en at-graf är hastigheten föremålet har just då. Precis som i fallet ovan kan arean om den är enkel beräknas med enkla former för rektanglar och trianglar men om den är mer komplicerad kan integration användas.
Ett exempel på när vi söker hastigheten i en acceleration-tid-graf finnes i exemplet nedan. Då visar vi även hur en lämplig indelning av arean under kurvan kan se ut.