Högsta höjd i en kaströrelse

Då vi tidigare lärt oss en del om kaströrelse vill vi nu givetvis lära oss mer om detta. Något som är viktigt i en kaströrelse är att ta reda på kastbanans högsta höjd.

\[ y= \frac{\sin^2{\alpha}\cdot{v_0}^2}{2g}\]

Härledning av formel för högsta höjd

I figur 1 illustreras vad som menas med höjd i vår kaströrelse.

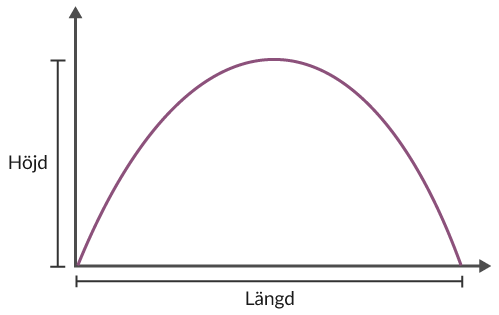
Med hjälp av detta tar vi fram vår formel för hastighet i y-led. Denna skrivs som

\[ v_y =v_0\sin{\alpha} - gt\]

Då vi vet att hastigheten är 0 i vändpunkten sätts detta in. Vi passar också på att döpa om tidpunkten för högsta höjd till \(t_h\) så att det är möjligt att se skillnad på variablerna senare.

\[ 0 =v_0\sin{\alpha} - gt_h\]

Tiden kan lösas ut genom att addera över den negativa termen och dividera med gravitationen. Då erhålls tidpunkten för högsta höjd som:

\[ t_h =\frac{v_0\sin{\alpha}}{g}\]

Vi tar sedan tiden ovan och stoppar in i formeln för kaströrelse som talar om var föremålet befinner sig i y-led efter en viss tid.

\[ y(t_h)=v_0\sin{\alpha}t_h - \frac{gt_h^2}{2}\]

Där har vi vår högsta höjd beräknad. Ovanstående metod tycker skribenten är rätt trevlig, men vi skulle kunna gå hela vägen och helt enkelt bygga en formel, oberoende av tiden genom att stoppa in tidsuttrycket helt och hållet, på följande vis:

\[ y(t_h)=v_0\sin{\alpha}(\frac{v_0\sin{\alpha}}{g}) - \frac{g(\frac{v_0\sin{\alpha}}{g})^2}{2}\]

Detta kan förenklas till genom gemensam nämnare och lite uppstädning i uttrycket till

\[ y= \frac{\sin^2{\alpha}\cdot{v_0}^2}{2g}.\]

Om du kastar något rakt uppåt har du en elevationsvinkel på \(\alpha = 90^{\circ}\). Detta ger \(\sin(90^{\circ}) = 1\) vilket gör formlerna något enklare att arbeta med.

Exempel på beräkning av högsta höjd

Sara har tagit sig till golfbanan och slår iväg en boll. Bollen har en utgångshastighet på 86.4 km/h och elevationsvinkeln är 38.9 grader.

Vi inleder med att omvandla hastigheten till meter per sekund. Detta görs genom att dividera med 3.6.

\[ 86.4~\text{km/h} = \frac{86.4}{3.6} = 24~\text{m/s}\]

I dess högsta läge är bollens hastighet 0.

\[ 0 =v_0\sin{\alpha} - gt_h\]

Vi kan lösa ut tiden ur detta eller plocka formeln ovan

\[ t_h =\frac{v_0\sin{\alpha}}{g} = \frac{24\sin(38.9^{\circ})}{9.82} \approx 1.53...~s\]

Golfbollen har sin maximala höjd vid 1.53 sekunder. Nu kan vi beräkna hur högt det egentligen är. Självklart tar vi med alla siffror när vi slår detta på miniräknaren men för att göra det lite snyggare avrundar vi i beräkningarna nedan.

\[ y(1.53...)=v_0\sin{\alpha}t_h - \frac{gt_h^2}{2} =24\sin(38.9^{\circ})\cdot1.53 - \frac{9.82\cdot1.53^2}{2} \approx  11.6~m.\]

Om vi använder formeln rakt av erhålls självklart samma värde.

\[ y= \frac{\sin^2{\alpha}\cdot{v_0}^2}{2g} = \frac{\sin(38.9^{\circ})^2\cdot24^2}{2\cdot9.82}\approx 11.6~m.\]

Anpassa vinkel efter höjd

David har en liten fin kanon med justerbar elevationsvinkel i sitt rum. Den kan skjuta ut kulor med en hastighet av 10 m/s. Davids kula får maximalt ha en höjd på 2.2 meter innan de slår i i taket. Vilken är den största elevationsvinkeln David kan ställa in på sin kanon så att kulorna inte slår i taket?

Vi sätter upp två ekvationer och försöker se hur vi kan lösa detta. Den första av dessa är

\[ y(t_h)=v_0\sin{\alpha}t_h - \frac{gt_h^2}{2}\]

Den andra ekvationen vi sätter upp är den som talar om att kulans hastighet i dess högsta punkt är 0.

\[ 0 =v_0\sin{\alpha} - gt_h\]

Vi söker en vinkel för att följande ska gälla \(y(t_h) = 2~m\) och \(v_0 = 10~m/s\).

Detta ger följande ekvationssystem

\[ \begin{cases} 2.2=10\sin{\alpha}t_h - \frac{9.82t_h^2}{2} \\ 0 =10\sin{\alpha} - 9.82t_h \end{cases}\]

Vi har två ekvationer och två okända variabler. Om du har en miniräknare som klarar ekvationssystem kan kan vi slå in följande och erhålla en vinkel på

\[ \alpha = 41 ^{\circ}.\]

Om du inte har en miniräknare som klarar ekvationssystem eller bara gillar att göra det för hand bjuder vi på en manuell lösning nedan.

Lösning av ekvationssystemet

Vi sätter upp ekvationssystemet med variabler för att detta är snyggare och gör det lättare att kontrollera om vi skulle göra något misstag.

\[ \begin{cases} y(t_h)=v_0\sin{\alpha}t_h - \frac{gt_h^2}{2} \\ 0 =v_0\sin{\alpha} - gt_h \end{cases}\]

Vi inleder med att lösa ut tiden ur den undre ekvationen

\[ t_h =\frac{v_0\sin{\alpha}}{g}.\]

Tiden vi löst ut sätts nu in i den övre ekvationen

\[ y(t_h)=v_0\sin{\alpha}(\frac{v_0\sin{\alpha}}{g}) - \frac{g(\frac{v_0\sin{\alpha}}{g})^2}{2}.\]

\[ a = 2\]

Detta kan förenklas till detta ganska enkla uttryck, vilket är uttrycket vi först kom fram till högre upp i posten.

\[ y= \frac{\sin^2{\alpha}\cdot{v_0}^2}{2g}\]

Det är nu möjligt att bryta loss sinus-kvadraten

\[ \sin^2{\alpha} = \frac{y(t_h)\cdot2g}{{v_0}^2}.\]

Vi drar kvadraroten ur båda leden. Var uppmärksam här, för här får vi två lösningar, men vi är bara intresserad av den positiva eftersom att det negativa skulle ge en negativ vinkel. Detta skulle innebära att kanonen var riktad ned i marken vilket är orimligt.

\[ \sin{\alpha} = \sqrt{\frac{y(t_h)\cdot2g}{{v_0}^2}} \]

Med hjälp av sinusinversen kan vinkeln beräknas i grader.

\[ \alpha = \arcsin\Big(\sqrt{\frac{y(t_h)\cdot2g}{{v_0}^2}}\Big)\]

Vi fyller i vår information och erhåller en vinkel.

\[ \alpha = \arcsin\Big(\sqrt{\frac{y(t_h)\cdot2g}{{v_0}^2}}\Big) = \arcsin\Big(\sqrt{\frac{2.2\cdot2\cdot9.82}{10^2}}\Big) \approx 41^{\circ}.\]

Givetvis går det utmärkt att lösa ut vinkeln direkt ur formeln och erhålla precis samma sak, men här är det vägen fram till lösningen som är poängen och inte en formel rakt upp och ner.