Jämvikt på en planka med en sned kraft
Hej! Idag ska vi räkna en exempeluppgift på kraftmoment om en pirat som går på plankan. Nedan följer uppgiften.
En planka vars masscentrum är placerat över relingen på ett piratskepp är fastsatt med ett rep i båten som har en högsta tillåten kraft på 5300 N. Repet har en vinkel på 25 grader från horisontalplanet och är fastsatt 1.0 meter in på plankan på skeppsidan. Hur långt kan en pirat med massan 96.2 kg maximalt gå ut på plankan innan repet ger vika och piraten hamnar i vattnet?
Figur och strategi för lösning
Denna uppgift är precis som många andra fysikuppgifter sprängfylld med information på ett par rader. Vi avlastar hjärnan genom att rita en bild över situationen.
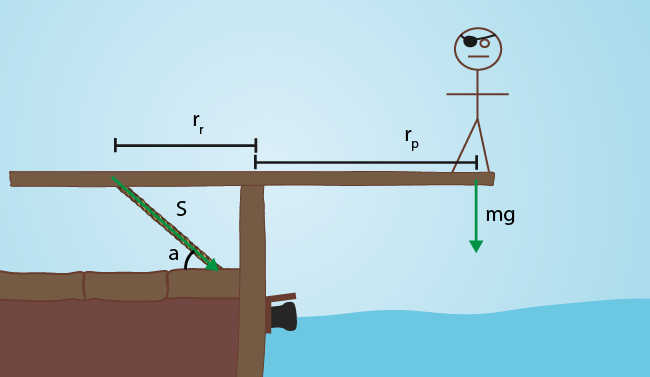
Vi kallar avståndet piraten kan gå för \(r_p\), avståndet till repet från vridpunkten döper vi till \(r_r=1.0\text{m}\), kraften kallar vi för \(S=5300\text{N}\) och vinkeln får heta \(a=25^{\circ}\).
För att beräkna hur långt ut piraten kan gå kommer vi anta att brädan precis innan den repet går av är i jämvikt. Då kan vi använda samma princip som på gungbrädorna under kraftmoment. Kraftmomenten medurs är då lika med kraftmomenten moturs.
Kraften från piraten kan vi få ut genom tyngdkraften och den antar vi är vinkelrät mot plankan. Kraften från repet är däremot inte vinkelrät så den behöver vi komposantuppdela för att få fram den vinkelräta komponenten.
Då masscentrumet för plankan sammanfaller med vridpunkten behöver vi inte tänka på den. Tänk att vridmomentet är kraften multiplicerat med avstånd och avståndet i detta fall är ju 0.
Komposantuppdela repkraften
Vinkeln är given och vi kan då använda trigonometri. En lämplig uppdelning av repkraften finns i figur 2.
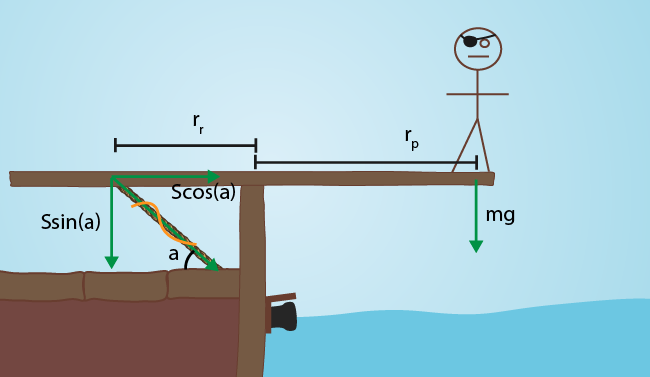
Den gula ormen markerar att vi ersatt den kraften med en vertikal och en horisontal kraft.
Nu kan vi börja ställa upp jämvikten av kraftmomenten.
Jämvikt av kraftmoment
Kraftmomentet som vill vrida plankan medurs är tyngdkraften piraten ger upphov till multiplicerat med avståndet till vridningspunkten, \(r_p\). Det är detta avstånd vi vill ta reda på.
\[ \text{Kraftmoment medurs} = mg r_p\]
Det kraftmoment som vill vrida plankan är den vinkelräta kraftkomponenten i repet multiplicerat avståndet där repet är fastsatt från vridcentrumet.
\[ \text{Kraftmoment moturs} = S\sin(a) r_r\]
Dessa sätter vi lika med varandra.
\[ mg r_p = S\sin(a) r_r\]
Dividera med \(mg\) på båda sidorna för att lösa ut avståndet.
\[ r_p = \frac{S\sin(a) r_r}{mg}\]
Sätt in numeriskt och vi får ut att piraten maximalt kan gå ut
\[ r_p = \frac{5300\cdot \sin(25^{\circ})\cdot1.0}{96.2\cdot 9.82} = 2.371...\text{m}.\]
Vi kan avrunda till 2 värdesiffror.
\[ r_p = 2.4\text{m}.\]
Om piraten går längre är summan av kraftmomenten inte längre noll, och då börjar plankan rotera och piraten blir blöt.