Acceleration-tid-graf för ett flygplan på startbanan

Hej! Vi har tidigare tittat på en hastighet-tid-graf och en sträcka-tid-graf, nu fortsätter vi med en acceleration-tid-graf för ett flygplan.

Låt oss säga att ett flygplan står still i början av startbanan vid tidpunkten \(t=0\). Sedan accelererar planet enligt grafen i figur 1 i 45 sekunder då flygplanet lyfter.

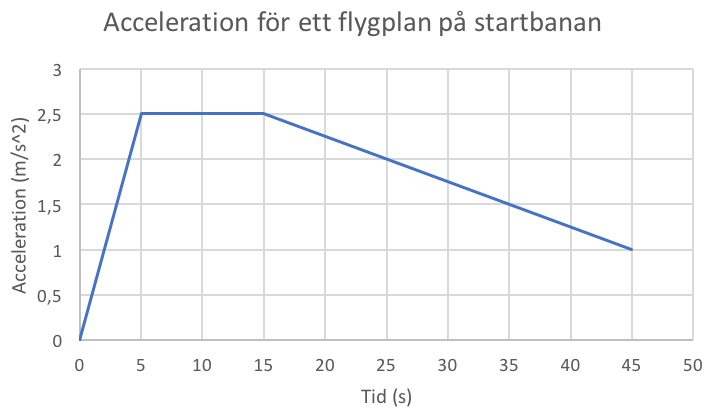
Vid vilken hastighet lyfter flygplanet?

Den stora frågan vi vill besvara är vid vilken hastighet planet lyfter. Hur detta kan gå till kan vi läsa mer om under grafer, men kortfattat nyttjar vi att acceleration multiplicerat med tid ger hastigheten och den kan vi integrera fram.

Hastigheten är arean under kurvan

Hastigheten får vi om vi integrerar, det är samma sak som att beräkna arean under kurvan. I detta fall har vi tur då kurvan är enkel och vi kan dela upp den i kända geometriska former. Förslagsvis delar vi upp den enligt figur 2 men om du hellre delar upp den på något annat sätt fungerar det också utmärkt.

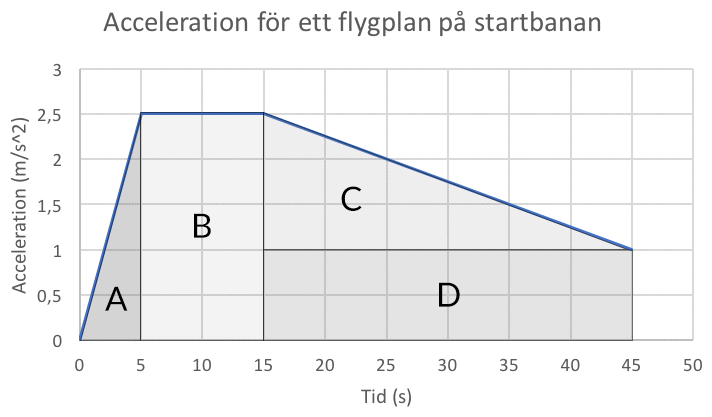
Vi sätter upp hastigheten som arean av två trianglar, A och C, samt två rektanglar A och D.

\[ v = A + B + C + D\]

Triangelns formel är basen multiplicerat med höjden dividerat på 2, och rektangeln har arean basen multiplicerad med höjden. Således får vi en hastighet på

\[ v = \frac{5\cdot2.5}{2} + {10}\cdot{2.5} + \frac{30\cdot1.5}{2} + 30\cdot 1.\]

Räknar vi ihop alla dessa,

\[ v = 83.75~\text{m/s.}\]

Vi kan räkna om det till kilometer per timme om vi vill genom att multiplicera med 3.6.

\[ v = 83.75\cdot3.6 = 301.5~\text{km/h.}\]

Om vi vill ha enheten som flygplanen använder själva ska vi svara i knop och behöver då dividera med \(1.852\).

\[ v = \frac{301.5}{1.852} = 162.797...~\text{knop.}\]

Flygplanet lyfter således med en hastighet av ungefär 163 knop.