Arkimedes Princip
Arkimedes princip är den mest grundläggande formeln inom vätskor och krafter. Den kan användas för att förklara varför det är så svårt att sänka ner en badboll under vattenytan och hur stora skepp kan flyta. Flytkraften \(F_\text{flyt}\) skrivs som
\[ F_\text{flyt} = \rho V g\]
där \(\rho\) är densiteten på den undanträngda vätskan, \(V\) är den nedsänkta volymen och \(g\) är tyngdaccelerationen. Flytkraften kommer från tryckskillnader i vätskan.
Översatt till svenska sade Arkimedes något i stil med...
Ett objekt nedsänkt helt eller delvis i en vätska får en flytkraft uppåt som är lika stor som tyngden på den av objektet undanträngda vätskan.
- Arkimedes
I figur 1 är det illustrerat hur Arkimedes princip fungerar om en tyngd sänks ner i en behållare med vätska.
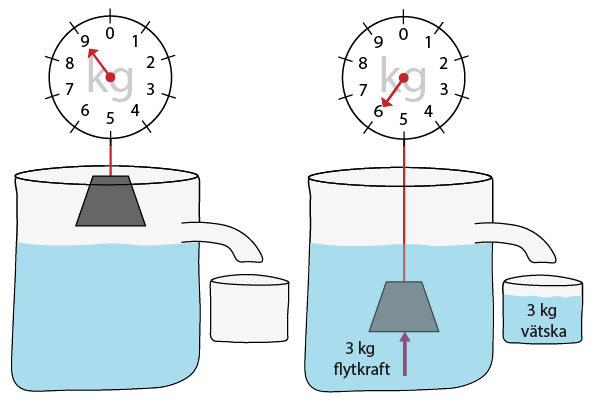
Om du någon gång slängt ner en stor sten i vattnet kanske du noterat att den sjunker långsammare än vad den gör i fritt fall i luften, vi kan använda Arkimedes princip för att räkna på detta.
Exempel på Arkimedes princip
Ett stenblock av marmor med volymen \(0.024~\text{m}^3\) och massan \(67~\text{kg}\) slängs i vattnet. Hur stor flytkraft får stenen från vattnet den tränger undan?
Vi använder givetvis Arkimedes princip. Densiteten för vatten brukar antas vara \(1000~\text{kg}/\text{m}^3\), volymen är given ovan och tyngdaccelerationen är \(9.82~\text{m}/\text{s}^2\).
\[ F_\text{flyt} = 1000\cdot 0.024 \cdot 9.82 = 235.6...\text{~N.}\]
Flyter stenen? Självklart inte. Vi kan rita ut krafterna som verkar och se i vilken riktning stenblocket rör sig i.
Hur fort sjunker stenen?
Vi ritar upp en sten och sätter ut de två krafterna som verkar på den.
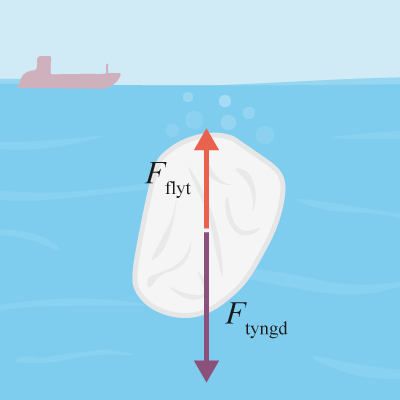
Vi vet enligt Newtons andra lag att summan av alla krafter är lika med massan multiplicerat med accelerationen.
\[ F_\text{res} = F_\text{flyt} - F_\text{tyngd}\]
Flytkraften kan vi skriva med Arkimedes princip som ovan, och tyngdkraften är stenens massa multiplicerad med tyngdaccelerationen. Således,
\[ ma = pVg - mg. \]
Vi kan dividera med stenens massa på båda sidorna och lösa ut accelerationen.
\[ a = \frac{\rho Vg }{m} - g\]
För in våra numeriska värden,
\[ a = \frac{1000\cdot 0.024\cdot 9.82}{67} - 9.82 = -6.302...~\text{m}/\text{s}^2\]
Stenblocket får en acceleration nedåt, som är långsammare än ett fritt fall, vilket är vad vi förväntar oss från vad vi förhoppningsvis sett i riktiga livet någon gång.
Arkimedes princip och jämvikt
Om vi konstruerar något som ska flyta är det av yttersta vikt att den resulterande kraften i vertikal riktning är 0. Det är så stora fartyg kan flyta. Skillnaden mot stenblocket ovan är att uttrycket då kan skrivas som
\[ 0 = F_\text{flyt} - F_\text{tyngd}.\]
vilket kan förenklas till
\[ F_\text{flyt} = F_\text{tyngd}.\]
Vi tittar på ett exempel på en brygga.
Flytkraft hos en brygga av lättbetong i vatten
En flytbrygga av lättbetong med densiteten \(\rho_b =550~\text{kg}/\text{m}^3\), har en bredd på \(b=3.0~\text{m}\), längd \(l=8.0~\text{m}\) och höjden \(h=0.4~\text{m}\). Hur långt sjunker bryggan ner i vattnet när den läggs i?
Vi ritar upp en bild över bryggan, det okända avståndet bryggan sjunker ner i vattnet kallar vi \(x\).
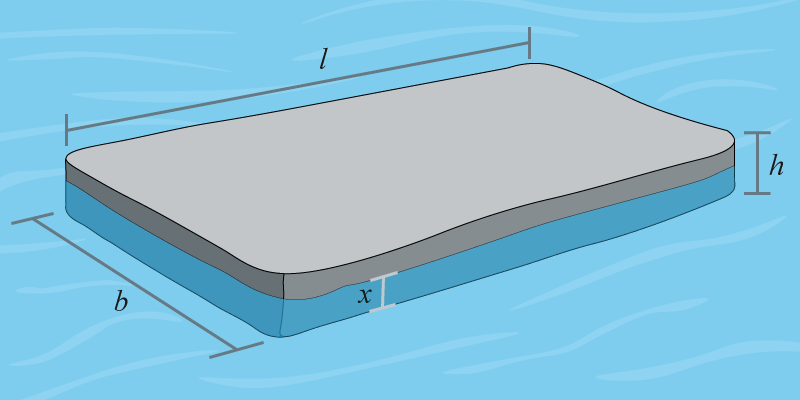
Därefter ritar vi bryggan från sidan och ritar ut de två krafter vi vet verkar på bryggan.

Vi ställer upp som ovan för jämvikt då vi vet att bryggan inte accelererar i något led när den ligger still.
\[ 0 = F_\text{flyt} - F_\text{tyngd}.\]
Vi för in för respektive kraft.
\[ 0 = \rho V g - mg \]
Vi vet inte massan \(m\) på bryggan. Däremot kan vi räkna ut den då vi vet volymen och densiteten. Volymen för ett rätblock är bredden multiplicerat med längden multiplicerat med höjden.
\[ m = \rho_b b l h. \]
Den undanträngda volymen \(V\) kan vi skriva som bredden multiplicerat med längden multiplicerat med \(x\), där \(x\) är djupet bryggan sjunker ner som vi ritat i figur 3.
\[ V = b l x \]
För att förtydliga, \(blh\) är volymen på hela flytbryggan, \(blx\) är volymen på delen som är under vattenytan. Detta sätter vi nu in i uttrycket.
\[ 0 = \rho b l x g - \rho_b b l h g\]
Det är väldigt grötigt just nu men vi kan dividera bort \(b l g\).
\[ 0 = \rho x - \rho_b h \]
Nu vill vi lösa för för \(x\).
\[ \rho x = \rho_b h\]
Dividera med vattnets densitet på båda sidorna.
\[ x = \frac{\rho_b h}{\rho}\]
Till sist sätter vi in de numeriska värdena. För densiteten på vatten använder vi \(\rho = 1000~\text{kg}/\text{m}^3\).
\[ x = \frac{550\cdot 0.4}{1000} = 0.22~\text{m}\]
Bryggan sjunker således ner 0.22m eller 22 cm i vattnet när den läggs i. En kul notering som du kanske märkte är att svaret är helt oberoende av bryggans bredd eller längd.
Arkimedes princip för zeppelinare och luftballonger
Arkimedes beskrev ursprungligen hur det fungerar för vätskor, men samma princip gäller för gaser. Detta innebär att vi kan räkna på luftballonger och zeppelinare med hjälp av Arkimedes princip. I detta fall är det undanträngda mediet luft.
Hur stor volym behöver luftballongen ha?
Andrée vill bygga en luftballong som lyfter med en svag acceleration uppåt på \(a=0.002~\text{m}/\text{s}^2\). Han använder av säkerhetsskäl helium med densiteten \(\rho_\text{He} = 0.1785~\text{kg}/\text{m}^3\). Ballongen behöver lyfta Andrée och en korg som tillsammans har massan \(m_k = 275~\text{kg}\). Hur stor volym helium behöver Andrèe anskaffa? Luften antas väga \(\rho_\text{L} = 1.225~\text{kg}/\text{m}^3\).
Vi inleder som brukligt med att rita en skiss över Andrées ballong och de krafter som verkar.
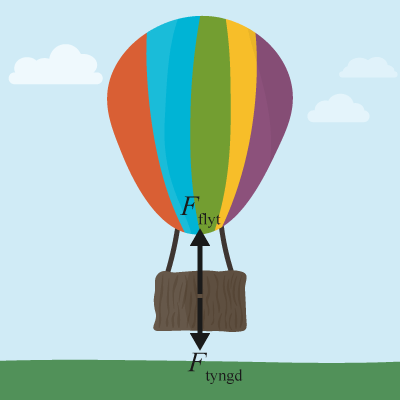
Vi sätter upp Newtons andra lag, summan av alla krafter är massan multiplicerat med accelerationen.
\[ F_\text{res} = F_\text{flyt} - F_\text{tyngd}\]
Flytkraften kommer från att ballongen tränger undan luften.
\[ F_\text{flyt} = \rho_\text{L} V g \]
där \(V\) är den sökta volymen på helium Andrée vill ta reda på. Tyngdkraften som vill dra ned ballongen består av korgen och massan på heliumet.
\[ F_\text{tyngd} = (\rho_\text{He}V + m_k)g\]
Den resulterande kraften är massan multiplicerat med accelerationen i enlighet med Newtons andra lag,
\[ F_\text{res} = (\rho_\text{He}V + m_k)a.\]
Vi sätter in detta i vårt ekvation ovan och löser för volymen \(V\).
\[ (\rho_\text{He}V + m_k)a = \rho_\text{L} V g - (\rho_\text{He}V + m_k)g\]
Nu är det rätt grötigt, om vi har en någorlunda avancerad räknare kan vi sätta in variablerna och lösa det numeriskt. Vi kommer ta den långa vägen och räkna för hand. Vi börjar med att utveckla alla parenteser, målet sedan är att samla alla termer med \(V\) på ena sidan.
\[ \rho_\text{He}V a + m_k a = \rho_\text{L} V g - \rho_\text{He}V g - m_k g\]
Flytta över \(\rho_\text{He}V a\) till högerledet och \(m_k g\) till vänster.
\[ m_k a + m_k g = \rho_\text{L} V g - \rho_\text{He}V g - \rho_\text{He}V a \]
Bryt ut \(V\) i högerledet.
\[ m_k a + m_k g = V(\rho_\text{L} g - \rho_\text{He} g - \rho_\text{He} a)\]
Dividera slutligen för att få volymen \(V\) ensam.
\[ V = \frac{m_k a + m_k g}{\rho_\text{L} g - \rho_\text{He} g - \rho_\text{He} a}\]
Till sist återstår bara att sätta in de numeriska värdena och räkna,
\[ V = \frac{275 \cdot 0.002 +275 \cdot 9.82}{1.225 \cdot 9.82 - 0.1785 \cdot 9.82 - 0.1785 \cdot 0.002}\]
vilket blir
\[ V = 262.843... ~\text{m}^3.\]
Således behövs det ungefär 263 kubikmeter helium för att Andrée ska lyfta med sin ballong med önskad acceleration. Då luften blir tunnare, dvs, densiteten minskar desto högre upp vi kommer finns det en höjd då ballongen slutar stiga uppåt. Den höjden går också att räkna ut med hjälp av data på hur luftens densitet förändras per höjdmeter. Om Andrée fyller sin ballong med mängden ovan kan han sannolikt inte räkna med några högre ballongfärder.