Längd i en kaströrelse
I denna genomgång ska vi titta på hur man kan beräkna längden av ett kast. Vi kommer att beräkna längden som föremålet färdats över marken, alltså inte kaströrelsens längd.
Kort och gott går detta till såhär:
- Föremålet befinner sig på höjden 0 vid två tillfällen. Det ena är vid tiden 0 sekunder och det andra är vid en okänd tid. Denna kan vi beräkna.
- Ta den beräknade tiden ovanför och multiplicera med hastigheten i x-led.
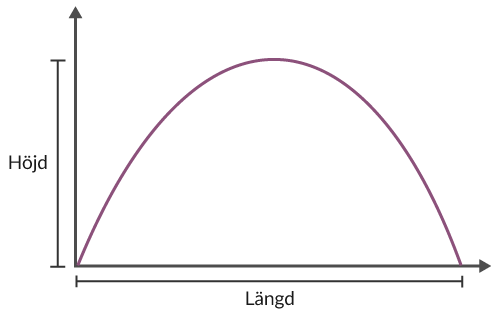
Formel för kastlängd
\[ \text{Längd} = \frac{{v_0}^2\sin{2\alpha}}{g}\]
Där \(v_0\) är utgångshastigheten, \(\alpha\) är elevationsvinkeln mellan utgångshastigheten och markplanet, och \(g\) är tyngdacceleration.
Var noggrann med att formeln kan endast kan användas när föremålet skjuts ut och landar på precis samma nivå. Se exempel nedan för skillnad.
Härledning av kastlängd
De formlerna vi kommer använda är följande två, mer om dessa finns under kaströrelse.
\[ \begin{matrix} y(t) =v_0\sin{\alpha}t - \frac{gt^2}{2} \\ x(t) = v_0\cos{\alpha}t \end{matrix}\]
Föremålet ska befinna sig på höjden \(y(t)=0\) för kastets längd.
\[ 0 =v_0\sin{\alpha}t - \frac{gt^2}{2} = t(v_0\sin{\alpha}-\frac{gt}{2})\]
Denna har lösningen att antingen är \(t=0\) eller så är
\[ v_0\sin{\alpha}-\frac{gt}{2} = 0.\]
Vi kan lösa ut tiden ur ovanstående
\[ t = \frac{2v_0\sin{\alpha}}{g}.\]
Formeln för ett kasts position i x-led
\[ x(t) = v_0\cos{\alpha}t = v_0\cos{\alpha}\cdot\frac{2v_0\sin{\alpha}}{g}\]
Med hjälp av dubblavinkelsatsen kan vi förenkla
\[ 2\cos{\alpha}\sin{\alpha} = \sin{2\alpha}\]
Vilket gör att hela uttrycket kan förenklas till
\[ x(t) = \frac{{v_0}^2\sin{2\alpha}}{g}\]
Exempel på beräkning av längden på ett kast
Anton slår iväg en golfboll med hastigheten 25 m/s och en elevationsvinkel på 32°. Hur långt slår Anton? Vi kommer ta hjälp av följande formel från kaströrelser:
\[ y(t)=v_0\sin{\alpha}t - \frac{gt^2}{2}\]
Det vi kommer utnyttja nu är att golfbollen kommer ha höjden y(t) = 0 vid två tillfällen. Dels vid utslaget, men även då golfbollen landar igen efter flygturen. Det är punkten där den prickade linjen slår i marken igen i figur 2.
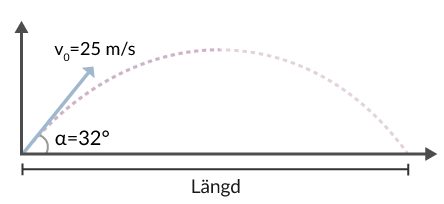
Vi får av detta följande ekvation då vi satt in vår hastighet och elevationsvinkel.
\[ 0 = 25\sin(32^{\circ})t - \frac{9.82t^2}{2}\]
Ovanstående ekvation kan lösas med hjälp av faktorisering, pq-formel eller kvadratkomplettering. I exemplet under finns ett exempel på hur en ekvation kan lösas med hjälp av pq-formeln.
Ekvationens lösningar skrivs som
\[ \begin{matrix} t_1 = 0 \\ t_2 = 2.69816... \approx = 2.7~s \end{matrix}\]
Den intressanta lösningen är den då tiden är ungefär 2.7 sekunder, för den första tidpunkten är den då golfbollen skjuts ut.
Med hjälp av följande formel från kaströrelsen kan vi nu beräkna kastets avstånd från utgångsläget.
\[ x(t)=v_0\cos{\alpha}t\]
Med våra värden insatta ger detta
\[ x(2.69816...) = 25\cos(32^{\circ})\cdot2.69816... = 57.2043... \approx 57~\text{meter.}\]
Golfslaget är således på 57 meter.
Om vi använder formeln rakt av blir resultatet givetvis samma.
\[ \text{Längd} = \frac{{v_0}^2\sin{2\alpha}}{g} = \frac{25^2\sin(2\cdot32^{\circ})}{9.82}=57.2043...\]
Svar: Golfslaget är 57 meter långt.
I exemplet nedan tittar vi på vad som händer när något landar på en annan nivå än där utgångshastigheten var.
Kast från en höjd
Frida står på sin balkong som är placerad 4.2 meter över marken. Då hennes mobiltelefon är långsam kastar hon den uppåt med en vinkel på 70° och en hastighet på 18 m/s. Mobiltelefonen lämnar hennes hand när den är 1.4 meter över balkongen. Se figur 3.
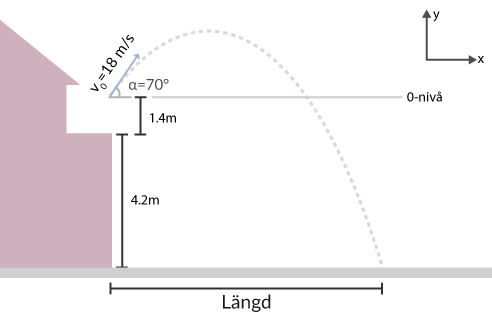
Vi vet nu att mobiltelefonen ska landa \(4.2 + 1.4 = 5.6\) meter under nollnivån.
Samma procedur kommer att användas som i den första exempeluppgiften. Först tar vi reda på hur lång tid mobiltelefonen är i luften och sedan multiplicerar vi det med den horisontella hastigheten.
\[ y(t)=v_0\sin{\alpha}t - \frac{gt^2}{2}\]
Här sätter vi in att \(y(t)\) ska vara ett negativt värde. Detta görs för att vi har definierat nollnivån (se figur 3) på den höjden som kastet startar.
\[ -(4.2 + 1.4)=18\sin(70^{\circ})t - \frac{9.82t^2}{2}\]
Detta är en andragradekvation som vi kan lösa med kvadratkomplettering, abc-formeln eller pq-formeln. Vi förenklar såpass mycket att den ser ut på samma sätt som pq-formeln.
\[ -5.6 =16.9145t - 4.91t^2\]
Nu flyttar vi över \(5.6\) till högerledet.
\[ 0 = 16.9145t - 4.91t^2 + 5.6\]
Division med \(-4.91\) av alla termer ger
\[ 0=-3.4449t + t^2 -1.1405\]
Detta in i pq-formeln,
\[ t=-\frac{(-3.4449)}{2} \pm \sqrt{(\frac{3.4449}{2})^2-(-1.1405)}.\]
Vi utvärderar båda rötterna numeriskt.
\[ \begin{cases} t_1 = -0.304213.. \approx -0.30~s \\ t_2 = 3.74911... \approx 3.7~s \end{cases}\]
Den första tiden är inte av värde för oss, för den är negativ, och visar var bollen skulle befunnit sig på marken i huset "åt andra sidan", i figur 3. Den andra tiden ska vi däremot använda i vår nästa ekvation.
\[ x(t)=v_0\cos{\alpha}t\]
Med värden insatta ger detta följande
\[ x(3.74911...)=18\cos(70^{\circ})\cdot3.74911... =23.0809...\approx 23~\text{meter.}\]
Svar: Mobiltelefonen har färdats 23 meter horisontellt.
Summering
Beräkna först tiden föremålet är i luften, oftast med formeln för position i x-led, och multiplicera sedan med den beräknade tiden med den horisontala hastigheten för att få kaströrelsens längd.