Medelhastighet hos en bil som accelererar och bromsar

Hej! För ett par månader sedan trillade denna in som kommentar på genomgången av acceleration. Uppgiften är särskilt bra då den innehåller räkning av hastighet, sträcka, tid och acceleration.

Vi kommer att dela upp det hela i tre etapper. Den första är när bilföraren accelererar från 60 km/h upp till 110 km/h, den andra är när han håller konstant hastighet, och den tredje etappen är när föraren bromsar ner till 0 km/h. Vi skissar en graf för bilens hastighet som funktion av tiden.

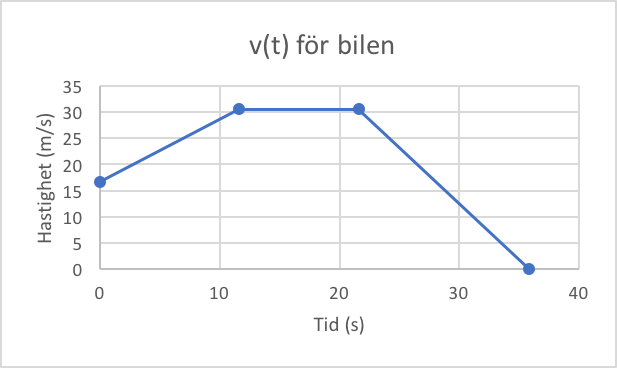
Vi inleder dock med att konvertera till alla km/h till m/s så har vi dessa gjorda redan.

\[ 60~\text{km/h} = \frac{60}{3.6}~\text{m/s} = 16.666...~\text{m/s}\]

\[ 110~\text{km/h} = \frac{110}{3.6}~\text{m/s} = 30.555...~\text{m/s}\]

Nu är vi redo att börja räkna första etappen.

Från 60 km/h upp till 110 km/h med 1.2 m/s²

Här behöver vi ta reda på tiden och sträckan bilen färdats. Sträckan kan vi räkna ut genom att använda

\[ s = v_0t + \frac{at^2}{2}\]

Den enda okända parametern i formeln ovan är tiden. Lyckligtvis kan vi beräkna denna genom att vi vet att accelerationen är hastighetsförändring dividerat på tid.

\[ a = \frac{\Delta v}{t}\]

Tiden är accelerationen multiplicerad med hastighetsförändringen.

\[ t =\frac{\Delta v}{a}\]

Vi sätter in numeriskt hastighetsförändringen och den givna accelerationen.

\[ t = \frac{30.555...-16.666...}{1.2} = 11.574...~\text{s}\]

Nu brukar vi formeln ovan för sträcka vid konstant acceleration.

\[ s = 16.666...\cdot 11.574... + \frac{1.2\cdot(11.574...)^2}{2}\]

Ett numeriskt svar på sträckan,

\[ s = 273.277...~\text{m.}\]

Nu kommer vi ihåg dessa värden. Vi kan för tydlighetens skull döpa om dessa och kalla de för etapp 1.

\[ s_1 = 273.277...~\text{m}\]

\[ t_1 =11.574...~\text{s}\]

Nu dags för nästa fas. Den konstanta hastigheten.

När föraren håller 110 km/h i 10 sekunder

Denna är något enklare. Vi kan ta reda på sträckan genom exempelvis SVT-triangeln eller lite algebra. Oavsett så kommer vi fram till att sträckan är hastigheten multiplicerad med tiden.

\[ s = vt\]

Vi för in våra värden för att få ett numeriskt svar.

\[ s = 30.555...\cdot10 = 305.555...~\text{m}\]

Precis som ovan döper vi om dessa för att få lite struktur. Vi kallar dessa för etapp 2.

\[ s_2 = 305.555...~\text{m}\]

\[ t_2 = 10~\text{s}\]

Från 110 km/h till 0 km/h på 14.2 sekunder

Nu trampar vår förare på bromsen. Vi använder ungefär samma metod som för etapp 1. Vi räknar ut retardationen,

\[ a = \frac{\Delta v}{t}\]

Vi för in numeriska värden,

\[ a = \frac{0 - 30.555...}{14.2} = -2.151...~\text{m/s}^2.\]

För omväxlingens skull kan vi använda en annan formel för att beräkna sträckan nu. Ur formelsamlingen hittar vi

\[ v^2 = {v_0}^2 + 2as.\]

Vi kan lösa ut sträckan ur denna som funktion av hastigheterna och accelerationen.

\[ s = \frac{v^2 - v_0^2}{2a}\]

Vi sätter in numeriska svar,

\[ s = \frac{0^2 - (30.555...)^2}{2\cdot(-2.151...)} =216.944...~\text{m.}\]

Denna kallar vi för etapp 3.

\[ s_3 =  216.944... ~\text{m}\]

\[ t_3 = 14.2~\text{s}\]

Beräkna medelhastigheten under hela förloppet

Nu börjar vi närma oss vårt slutgiltiga mål. För att få medelhastigheten summerar vi hela sträckan och dividerar med summan av hela tiden. Idag är vi extra tydliga och använder ett sträck över hastigheten för att markera medelhastighet.

\[ \overline{v} = \frac{s_1+s_2+s_3}{t_1+t_2+t_3}\]

Vi för in respektive värde ovan.

\[ \overline{v} = \frac{273.277...+305.555...+216.944... }{11.574...+10+14.2}\]

Slår vi in detta på en räknare ges

\[ \overline{v} = 22.244...~\text{m/s.}\]

Omvandla detta till km/h genom att multiplicera med 3.6.

\[ \overline{v} = 80.080...~\text{km/h.}\]

Det minsta vi har är två gällande siffror, således kan vi med gott samvete svara att bilens medelhastighet under förloppet varit 80 km/h.

\[ \overline{v} \approx 80~\text{km/h.}\]

Grafisk jämförelse med medelhastighet

Vi ritar in medelhastigheten i samma diagram som i figur 1 som en liten extra bonus.

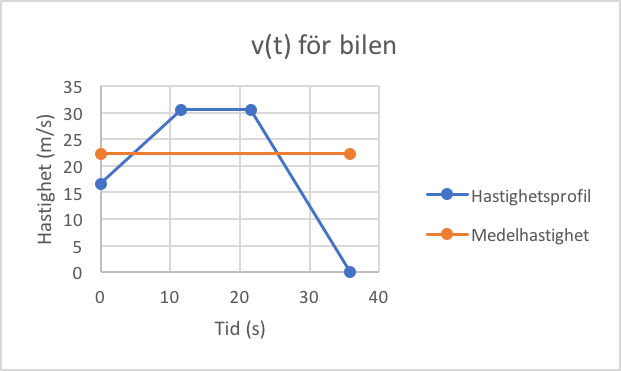
Detta kan vi tolka som att arean under den blåa kurvan är samma som arean under den orangea kurvan.