Exempel på kaströrelse

I en tidigare genomgång har vi skrivit om kaströrelser och lite hur dessa formler kan tas fram. I denna guide tänkte vi visa hur de kan användas i praktiken. Formlerna är följande:

\[ \begin{matrix} x(t)=v_0\cos{\alpha}t \\ y(t)=v_0\sin{\alpha}t - \frac{gt^2}{2}\\ v_x(t)=v_0\cos{\alpha} \\ v_y(t)=v_0\sin{\alpha} - gt\\ v = \sqrt{v_x^2 + v_y^2} \end{matrix}\]

Var befinner sig bollen i en kastparabel?

En boll sparkas med en hastighet av 10 m/s och en elevationsvinkel på 30° som figur 1 visar.

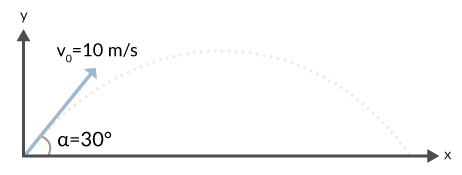
Vi ska besvara följande frågor:

• Vilken punkt befinner sig bollen i efter 0.4 sekunder?
• Vad är bollens hastighet i x-led respektive y-led efter 0.4 sekunder?
• Vad är bollens fart efter 0.4 sekunder?

I vilken punkt befinner sig bollen efter 0.4 sekunder?

Vi använder de två översta formlerna. Först beräknar vi bollens punkt i x-led.

\[ x(t)=v_0\cos{\alpha}t\]

Med våra värden ger detta en position i x-led

\[ x(0.4)=10\cos(30^{\circ})\cdot0.4\approx 3.5~\text{meter}.\]

För att beräkna bollens position i y-led använder vi följande formel.

\[ y(t)=v_0\sin{\alpha}t - \frac{gt^2}{2}\]

På samma sätt som i x-led sätter vi in vår hastighet, vinkel och tid.

\[ y(0.4)=10\sin(30^{\circ})\cdot0.4 - \frac{9.82\cdot0.4^2}{2} \approx 1.2~\text{meter}.\]

Svar: Bollen befinner sig i punkten (3.5, 1.2). I skrift blir det att bollen befinner sig 3.5 meter till höger från utgångsläget och 1.2 meter upp i luften.

Vad är bollens hastighet i x-led respektive y-led efter 0.4 sekunder?

Vi använder formlerna för hastighet i respektive riktning. Först beräknar vi hastigheten i x-led.

\[ v_x(t)=v_0\cos{\alpha}\]

Med vår utgångshastighet och vinkel insatt ger detta:

\[ v_x(0.4)=10\cos(30^{\circ}) = 8.66025... \approx 8.7 ~\text{m/s}\]

Nu går vi vidare och beräknar hastighet i y-led, med följande formel.

\[ v_y(t)=v_0\sin{\alpha} - gt\]

Våra värden på utgångshastighet och elevationsvinkel ger oss en hastighet

\[ v_y(0.4)=10\sin(30^{\circ}) - 9.82\cdot0.4 = 1.072 \approx 1.1~\text{m/s.}\]

Svar: Bollens hastighet i x-led är 8.7 m/s och i y-led 1.1 m/s.

Vad är bollens fart efter 0.4 sekunder?

Nu vill vi veta hur fort bollen går, utan att ta hänsyn till någon axel på ett koordinatsystem. Detta gör vi med den sista formeln.

\[ v = \sqrt{v_x^2 + v_y^2}\]

Vi använder de exakta värdena ur uppgift 2 för att få fram en korrekt fart.

\[ v = \sqrt{(8.66025...)^2 +1.072^2} = 8.72634... \approx 8.7~\text{m/s.}\]

Svar: Bollens fart är 8.7 m/s efter 0.4 sekunder.