Newtons andra lag - kraft är lika med massan gånger acceleration
Newtons andra lag säger att den resulterande kraften är detsamma som massan multiplicerad med accelerationen.
\[ \vec{F}= ma\]
Om du söker det som Newton egentligen skrev så formulerades det som
\[ \vec{F}= \frac{d\vec{p}}{dt}\]
I skrift skulle det skrivas som att kraften är förändringen av rörelsemängd. Mer om detta finns att läsa längst ner.
Enheten för kraft är Newton.
\[ 1~\text{N} = 1~\frac{\text{kg}\cdot\text{m}}{s^2}\]
Det är lätt, speciellt i början att anta att alla krafter kan skrivas som F=ma, detta är fel. Det är enbart den resulterande kraften som är lika med massan multiplicerad med accelerationen.
Lådor acceleration med hjälp av Newtons andra lag
Två lådor dras framåt med varsin kraft på 8N. De två lådorna har massan 2 kg respektive 4 kg. Vilken låda accelererar snabbast?
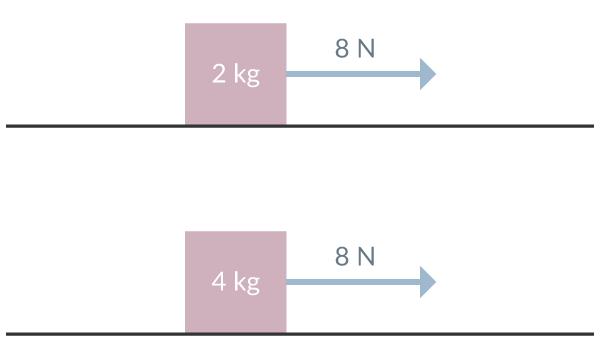
Vi har ritat lådorna i samma bild, men de är inte staplade på varandra utan ska ses som enskilda.
Beräkna accelerationen 2 kg-lådan
Med hjälp av Newtons andra lag kan vi beräkna accelerationen.
\[ F = ma\]
Då vi har kraften (F) och massan (m) kan vi enkelt sätta in det i formeln ovan och lösa ekvationen
\[ 8 = 2a.\]
Ekvationen kan vi lösa genom att dividera med 2 på båda sidorna.
\[ a = \frac{8}{2} = 4~m/s^2.\]
Accelerationen för lådan som väger 2 kg är således 4 m/s2.
Beräkna accelerationen för 4 kg-lådan
Vi gör precis på samma sätt som för den första lådan.
\[ F = ma\]
Då vi vet vilken kraft och massa som vi har kan vi räkna ut accelerationen
\[ 8 = 4a.\]
Ekvationen löses genom att dividera med 4 på båda sidorna.
\[ a = \frac{8}{4} = 2~m/s^2.\]
Lådan som väger 4 kg har en acceleration på 2 m/s2.
Detta innebär givetvis att lådan som har en massa på 2 kg accelererar snabbare än lådan med massan 4 kg.
Beräkna massan ur Newtons andra lag
Den resulterande kraften på en bil är 2400 Newton och bilen accelererar med 1.6 m/s2. Hur stor massa har bilen?
Den enda kraften måste vara den resulterande kraften. Med hjälp av Newtons andra lag vet vi att
\[ F = ma\]
Om vi dividerar med accelerationen på båda sidorna av likhetstecknet erhålls
\[ m = \frac{F}{a}\text{.}\]
Med våra värden insatta får vi accelerationen
\[ m=\frac{F}{a} = \frac{2400}{1.6} = 1500~\text{kg.}\]
Bilen har således en massa på 1500 kg.
Flera krafter och Newtons andra lag
I en låda med massan 10 kg fästs fyra stycken rep. På vänster sida om lådan drar två personer med en kraft av 130N respektive 180N, på höger sida dras lådan av två personer med krafterna 120N och 160N. Hur hur är lådans acceleration? Bortse från friktion och övriga krafter.
Vi inleder med att rita en bild av situationen, se figur 2 nedan.
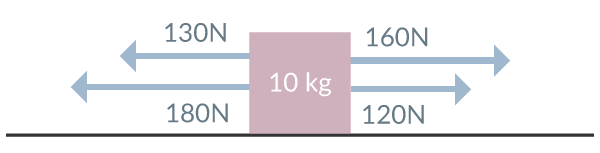
Vi har endast krafter horisontalt, vilket gör det hela lite enklare. Vi beräknar den resulterande kraften genom att summera alla krafter, därefter beräknar vi accelerationen.
\[ \sum{F = F_1 + F_2 + F_3 + F_4} = ma\]
\(\Sigma\) kallas för sigma och är en bokstav i det grekiska alfabetet. Vi använder detta tecken om vi vill addera ihop en massa termer för att spara plats, tid och göra beräkningarna lite snyggare.
I vårt fall ovan hade vi bara 4 krafter, vilket gör det helt okej att skriva ut allihopa, men om över hundra krafter verkar kan det bli lätt ta mycket plats och bli svåröverskådligt.
I början på gymnasiet är det sannolikt att summatecknet inte introducerats, därav denna ruta av information. Om du ännu inte fått lära dig summatecknet av din lärare kan detta vara ett fint sätt att smyga in hur ambitiöst du studerat inför provet.
Vi börjar med att summera ihop krafterna.
\[ \sum{F} = -130N - 180N + 120N + 160N = -30N\]
Minustecknet kommer av att de två som drar lådan åt vänster drar åt negativ riktning, om vi tänker att det hela sker på en tallinje.
Accelerationen kan vi beräkna på samma sätt som med de första lådorna, det vill säga att vi dividerar med massan.
\[ \sum{F} = ma\]
Division med massan på båda sidor ger
\[ \frac{\sum{F}}{m} = a.\]
Nu är vi redo att sätta in våra värden.
\[ a = \frac{-30}{10} = -3~m/s^2.\]
Lådan får en negativ acceleration på 3 m/s2.
Rörelsemängd eller massa och acceleration?
Newtons andra lag formulerade av Newton som
\[ \vec{\boldsymbol{F}}= \frac{d\vec{\boldsymbol{p}}}{dt}\]
vilket är en förenkling som genomförs genom att anta att massan är kontant. Detta sker på följande vis
\[ \vec{\boldsymbol{F}}= \frac{d\vec{\boldsymbol{p}}}{dt} = \frac{d(m\vec{\boldsymbol{v}})}{dt} = m\frac{d\vec{\boldsymbol{v}}}{dt} = m\vec{\boldsymbol{a}}.\]
Detta sätter begränsningar på hur nära verkligheten vi kommer i våra beräkningar för föremål som på ett eller annat sätt förändrar sin massa. Ett exempel på det är en rymdraket som snabbt förändrar sin massa under starten.
Om du undrar vad \(d\) står för i bråket, så kan det ses som en väldigt liten förändring av rörelsemängd dividerat med en väldigt liten förändring av tid.
På Fysikguiden.se kommer vi dock alltid att anta att massan är konstant om inte annat sägs.