Fjäderns svängningstid

Formeln för fjäderns svängningstid skrivs som

\[ T = 2\pi \sqrt{\frac{m}{k}}\]

Där \(T\) är tiden och \(m\) är massan och \(k\) är fjäderkonstanten.

Tiden för en period

När vi menar en period menar vi att massan hinner göra en svängning och sedan tillbaka till ursprungsläget.

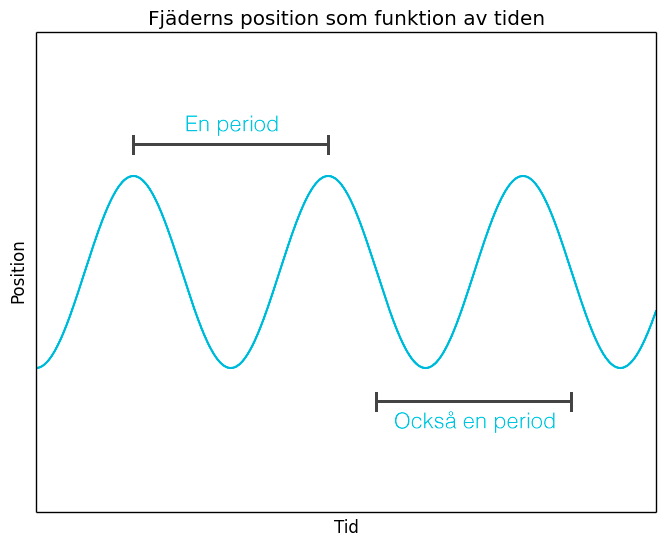
Det spelar således ingen roll var perioden börjar, så länge den slutar på samma ställe. Om vi tittar på fjäderns rörelse och försöker räkna perioder kan det vara lättare att ta topplägen eller bottenlägen, medan vi i något annat sammanhang kanske hellre har att en period startar då positionen inte är förskjuten från jämviktsläget.

Exempelberäkning av svängningstid för en fjäder och massa

En fjäder med fjäderkonstanten 44.6 N/m hängs upp i taket. Längst ner i fjädern sätts en massa på 2.17 kilo, hur lång tid tar en svängningstid?

Vi nyttjar formeln rakt av helt enkelt. In med massan och fjäderkonstanten i formeln.

\[ T = 2\pi \sqrt{\frac{2.17}{44.6}} \approx 1.39~\text{s.}\]

En svängning, från ett läge och tillbaka till samma läge tar således ungefär 1.39 sekunder.

Konstruera en sekundmätare med hjälp av en fjäder

Vi vill skapa oss en sekundmätare med hjälp av en fjäder och en massa. Idéen är att sätta en massan i rörelse så att varje period är så nära en sekund som möjligt. Om vi har en fjäderkonstant på 62.23 N/m, hur stor massa behövs hängas på för att få en svängningstid på en sekund?

Vi startar med formeln som vanligt, och ska lösa ut \(m\).

\[ T = 2\pi \sqrt{\frac{m}{k}}\]

Först kan vi dividera med \(2\pi\).

\[ \frac{T}{2 \pi} = \sqrt{\frac{m}{k}}\]

Nu kan vi kvadrera båda leden för att få bort roten-ur-tecknet på högersidan.

\[ \Big(\frac{T}{2 \pi}\Big)^2 = \frac{m}{k}\]

Multiplicera upp fjäderkonstanten och vi är framme.

\[ m = k \Big(\frac{T}{2 \pi}\Big)^2\]

Vi sätter in vår fjäderkonstant och tiden en sekund,

\[ m =62.23\cdot\Big(\frac{1}{2 \pi}\Big)^2 \approx 1.576~\text{kg.}\]

Om vi hänger på någon pryl som har massan 1.576 kg har vi således byggt oss en sekundräknare. Nu tar varje hela svängning en sekund.

Introduktion till härledning av formeln

Härledningen av formeln för fjäderns periodtid kräver att vi hämtar lite matematik från Matematik 4, och då de flesta inte kommit dit när de kommit till fjäderavsnittet i fysiken blir härledningen något lidande av detta. Såhär kan det i stora drag gå till.

Newtons andra lag gäller även för fjädern och för en fjäderkraft. Det betyder att summan av alla krafter är lika med massan multiplicerat med accelerationen.

\[ \sum F = ma\]

De krafter som finns är Hookes lag, fjäderkraften. Notera minustecknet här, läs mer om det under fjäderkraftsidan.

\[ - kx = ma\]

Accelerationen är andraderivatan av sträckan \(x\). Således kan den skrivas som

\[ - kx = mx''\]

Där det är underförstått att \(x\) beror på tiden. Nu har vi fått oss en ordinär differentialekvation. Om vi flyttar över allt till ena sidan kan det se ut såhär,

\[ 0 = mx'' +kx. \]

Den är mycket snarlik de differentialekvationer som löses i Matematik 4, och om vi använder detta kommer vi fram till att vinkelfrekvensen är

\[ \omega = \sqrt{\frac{k}{m}}.\]

Det är också i stegen ovan matematiken kan bli mycket knepig, därav vänder vi lite lätt bort blicken från det. Därifrån går vi bara från vinkelfrekvens, till frekvens och tillslut till periodtid.

\[ T = 2\pi \sqrt{\frac{m}{k}}\]

Observera att härledningen inte är fullständig från början till slut utan är tänkt som stöd för gymnasial nivå.