Newtons första lag
Newtons första lag formulerades ursprungligen på latin, vi har dock översatt den till svenska och presenterar den som nedanstående.
Om summan av krafterna som verkar på en kropp är noll kommer hastigheten att vara konstant (vilket inkluderar hastigheten noll) och ha noll acceleration.
- Isaac Newton
Ovanstående definition är dessvärre ganska svår att förstå om man är ny, därför kan vi skriva en förenklad version med ett exempel.
Förenklad version av Newtons första lag
Om krafterna som verkar på exempelvis en bil är lika så kommer bilen antingen att åka med samma hastighet eller stå helt still.
Newtons första lag på en bil som kör en sträcka
Nu ska vi titta lätt på en bil som rör sig.
Bilen står still
I bilens startskede står bilen stil, bilen har ingen motorkraft framåt och ingen motorkraft bakåt. Summan av krafterna är således 0. Enligt Newtons första lag så står bilen still.

Bilen gasar
Bilens förare gasar på och bilen ökar sin hastighet, samtidigt byggs ett luftmotstånd upp. Vi ritar ut motorkraften och luftmotståndet som två krafter i motsatt riktning.
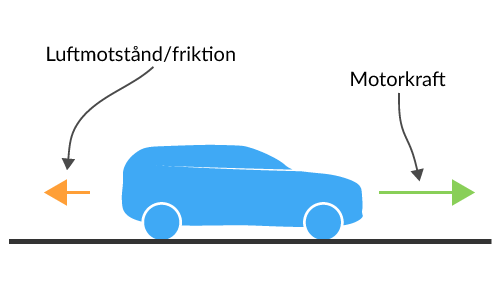
I detta skede är motorkraften större än luftmotståndet. Summan av krafterna är alltså inte 0, och vi vet då enligt Newtons första lag att bilen inte kan stå still eller färdas i konstant hastighet.
Även om vi inte hur stora krafterna är vet vi att summan inte är 0, då pilarna är olika stora, vilket symboliserar att krafterna är olika stora
Motorkraften och luftmotståndet är lika stora
Bilen har nu nått hastigheten som står på skylten bredvid vägen. Föraren ger lika mycket gas som behövs för att bilen ska åka med samma hastighet hela tiden.
Vi ser att summan av krafterna är 0 då pilarna är lika stora och riktade åt motsatt håll, och enligt Newtons första lag håller bilen nu en konstant hastighet. Nedanför illustreras situationen.
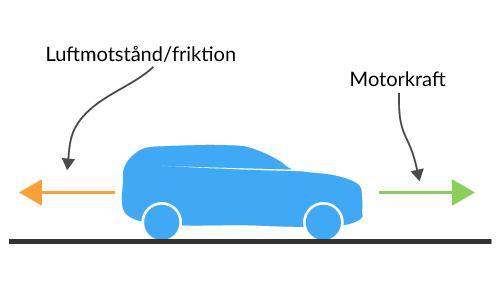
Föraren släpper gasen helt och hållet
Föraren släpper sin fot från gaspedalen och låter luftmotståndet sakta ner bilen. Nu finns endast luftmotståndet. Enligt Newtons första lag så färdas inte bilen i konstant hastighet och den är inte heller stillastående, då summan av krafterna inte är 0.
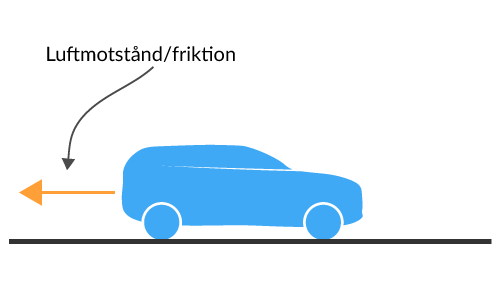
När kan vi använda Newtons första lag?
Newtons första lag är användbar på situationer då något står still eller rör sig med konstant hastighet, för då vi vi att summan av alla krafter är 0. Vi kan dela upp i komposanter och använda Newtons första lag för respektive komposant. Vanligast i gymnasiet och början på universitet är att dela upp krafterna i x-led, y-led och ibland även z-led.
Okända krafter med hjälp av Newtons första lag
Ett flygplan med massan 200 ton flyger på 40000 fot med en konstant hastighet på 500 knop. Den totala kraften i motorerna är 560 kN. Beräkna luftmotståndet och lyftkraften som verkar på planet.
Vi ritar en bild över flygplanet och ritar ut krafterna.
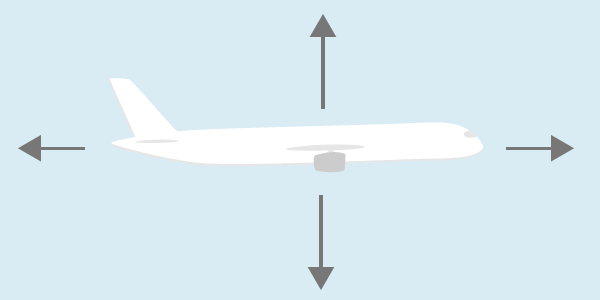
Vi delar upp situationen. Först tittar vi på kraftsituationen i x-led.
Då Newtons först lag gäller och vi vet att hastigheten är konstant så måste luftmotståndet vara precis lika stort som kraften motorerna genererar. Kraften från luftmotståndet är således 560 kN.
Nu tittar vi på situationen i y-led. I vänsterledet skriver vi våra krafter, vi sätter positiv riktning uppåt som ett koordinatsystem har. I högerledet sätter vi 0, eftersom vi vet att summan av krafterna är 0.
\[ \text{Lyftkraft} -\text{Tyngdkraft} = 0\]
Vi flyttar över Tyngdkraften till höger sida, och vi får då sambandet
\[ \text{Lyftkraft} = \text{Tyngdkraft}\]
Tyngdkraft kan också skrivas som
\[ F_{mg} = mg\]
Vilket ger vår lösning för flygplanet ovan
\[ \text{Lyftkraft} = mg\]
Med massan,
\[ m = 200~\text{ton} = 200~000~\text{kg}.\]
och konstanten för tyngdacceleration i Stockholm \(g \approx 9.82~m/s^2.\)
Nu är vi framme och kan beräkna lyftkraften.
\[ \text{Lyftkraft} = 200~000\cdot 9.82 = 1964000 \text{N} \approx 1.96 \text{MN.}\]
Vi kommer använda Newtons första lag frekvent på Fysikguiden.se, så bli inte förvånad om du ser referenser hit lite varstans.