Impuls

Hej! på denna sida tittar vi närmare på impuls, impulslagen och hur detta sitter ihop med rörelsemängd inom fysiken. För dig som är i början av gymnasiet är en impuls lika med en konstant kraft multiplicerat med ett tidsintervall.

\[ I = F\Delta t\]

Allmänt, om kraften inte är konstant kan vi säga att en impuls är lika med arean under en kraft-tidsgraf mellan två satta tidpunkter. Se avsnittet om impuls som area och integral längre ner. Impuls är liksom rörelsemängd en vektor. Den har en storlek och en riktning.

Enheten Newtonsekund

Enheten för impuls är newtonsekund, ofta förkortat till Ns.

\[ I = 1~\text{Ns.}\]

En newtonsekund är precis lika med en kgm/s som är enheten för rörelsemängd. Det finns givetvis en koppling mellan impuls och rörelsemängd, nämligen impulslagen nedan.

Impulslagen

En impuls är lika med en ändring av rörelsemängd. Det innebär att om en kraft verkar en tid förändrar det rörelsemängden på föremålet.

\[ I = \Delta p = p_2 - p_1 \]

I formeln ovan är \(p_2\) rörelsemängden efter kraften verkat, och \(p_1\) är rörelsemängden före.

Det är viktigt att komma ihåg att impuls, liksom rörelsemängd är en vektor. Därför måste vi hålla koll på hur impulsen är riktad.

Exempel på impuls och rörelsemängd

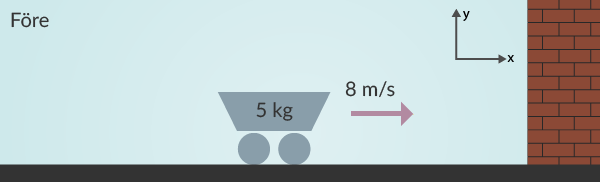
En vagn på en friktionsfri bana har massan 5.0 kg och hastigheten 8.0 m/s. Den åker rakt in i en vägg och studsar tillbaka med hastigheten 6.0 m/s. Vagnen är i kontakt med väggen i 0.020 sekunder. Hur stor är storleken på medelkraften som väggen påverkar vagnen med?

Det är inte givet vilken riktning vagnen åker åt, vi antar därför att vagnen åker åt höger. Tanken här att vi vet att impulsen är lika med en förändring av rörelsemängd, samtidigt som impulsen också är lika med en medelkraft under en tid. Först ritar vi en bild hur det ser ut före och efter.

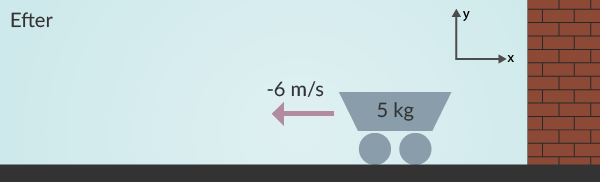
En bild efter vagnen har studsat in.

Vi ställer upp att impulsen är lika med en förändring av rörelsemängd.

\[ F\Delta t = p_2 - p_1\]

Kraften \(F\) fås genom att båda leden divideras med tiden \(t\).

\[ F = \frac{p_2 - p_1}{\Delta t}\]

Nu till rörelsemängden före och efter studsen i väggen. Vi börjar med rörelsemängden före, \(p_1\).

\[ p_1 = mv_1\]

Detta då vagnen är på väg åt höger, och det har vi definierat som positiv riktning med pilen uppe högra hörnet på figurerna. Rörelsemängden efter studsen,

\[ p_2 = m(-v_2)\]

Denna rörelsemängd är negativ, då hastigheten är negativ, och den är på väg åt motsatt riktning den vi definierat som positiv.

In i uttrycket för kraft.

\[ F = \frac{m(-v_2) - mv_1}{\Delta t}\]

Nu kan vi beräkna ett numeriskt värde på kraften.

\[ F = \frac{5.0\cdot(-6.0) - 5.0\cdot8.0}{0.020}\]

Vilket uträknat ger en negativ kraft,

\[ F = - 3500~\text{N.}\]

Detta betyder att kraften är riktad åt vänster. Storleken på kraften är absolutbeloppet av ovanstående kraft, dvs 3500 N. Om vi hade antagit att vagnen åkt åt vänster hade vår kraft fått samma storlek.

Svar: Storleken på kraften är 3500 N. Om vi vill svara med korrekt antal gällande siffror behöver vi avrunda uppåt till 4000 N.

Impuls som area under graf

Ett mer allmänt sätt att definiera impuls är att integrera kraften över en viss tid. Då behöver inte kraften som i exemplet ovan vara konstant utan kan variera.

\[ I = \int F dt\]

Kort sagt kan vi säga att om vi har ett diagram för hur kraften förändras med tiden är impulsen arean under grafen.

Exempel på area under graf med figurer

I figur 3 visas ett kraft-tid-diagram. Vi vill beräkna impulsen.

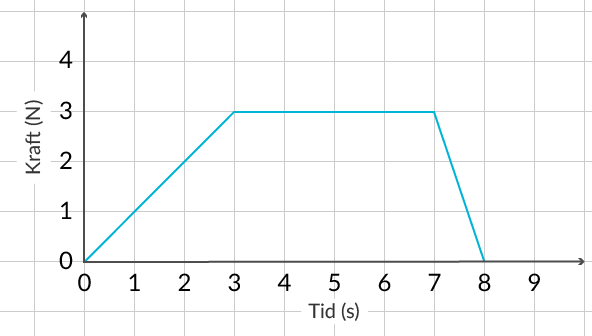
Vi vet att impulsen är lika med arean under kurvan. I figur 4 har vi ritat in vilken area det rör sig om.

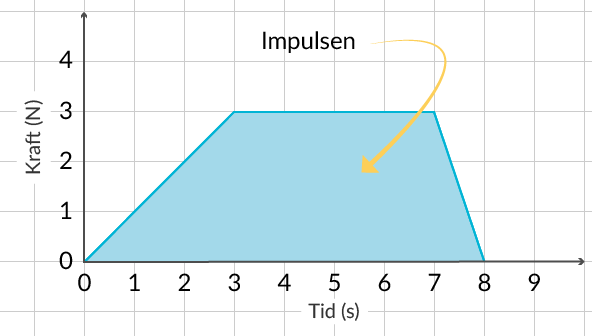
Det är möjligt att ta reda på en funktion eller flera funktioner som beskriver kurvan och sedan integrera denna funktion över tiden. Detta är dock lite knepigare, vi kommer istället nyttja att arean kan delas upp i tre områden, två trianglar och en rektangel.

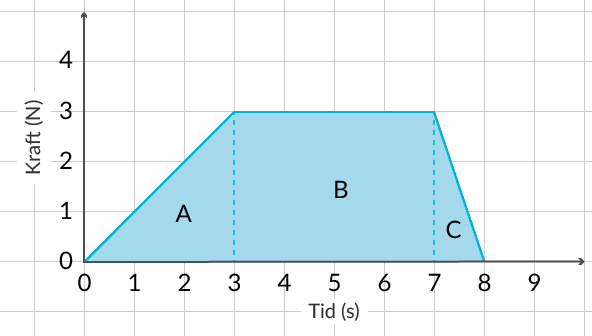
Vi kan således skriva upp impulsen som summan av areorna för \(A\), \(B\) och \(C\).

\[ I = A + B + C\]

Formlerna för triangelns area, basen multiplicerat med höjden dividerat med 2, samt formeln för rektangelns area, basen multiplicerat med höjden bör finnas någonstans i hjärnkontoret.

\[ I = \frac{3\cdot3}{2} + 4\cdot3 + \frac{1\cdot3}{2}\]

Vi kan förenkla impulsen till

\[ I = 18~\text{Ns.}\]

Impuls som integral

Nu ska vi räkna en exempeluppgift där vi kommer att integrera. Integraler dyker upp i Matematik 3 för dagens gymnasieskola och Matematik D för det gamla systemet. Beroende på schema och skola är det möjligt att impulsavsnittet gås igenom före integraler, varvid nedanstående kan framstå som grekiska för en icke grekisk-talande person.

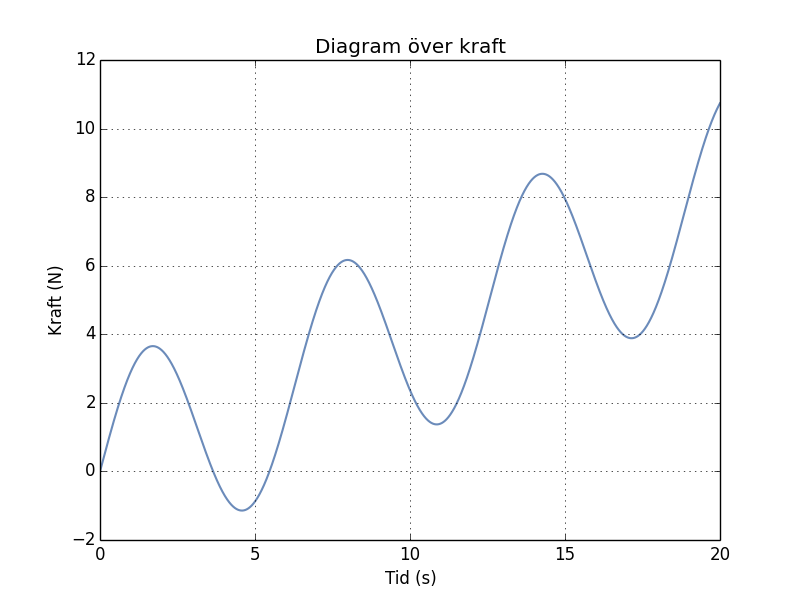
Nu till själva exemplet. Låt oss säga att kraften beskrivs med funktionen

\[ F(t) = 3\sin{t} + 0.4t.\]

Vi vill beräkna impulsen mellan tiden \(t_1 = 2\) och \(t_2 = 13\) sekunder. Först skissar vi upp funktionen i ungefär det området vi är intresserade av.

Vi kommer ihåg att impulsen fås om vi integrerar över området. Detta området är blåmarkerat i figur 7.

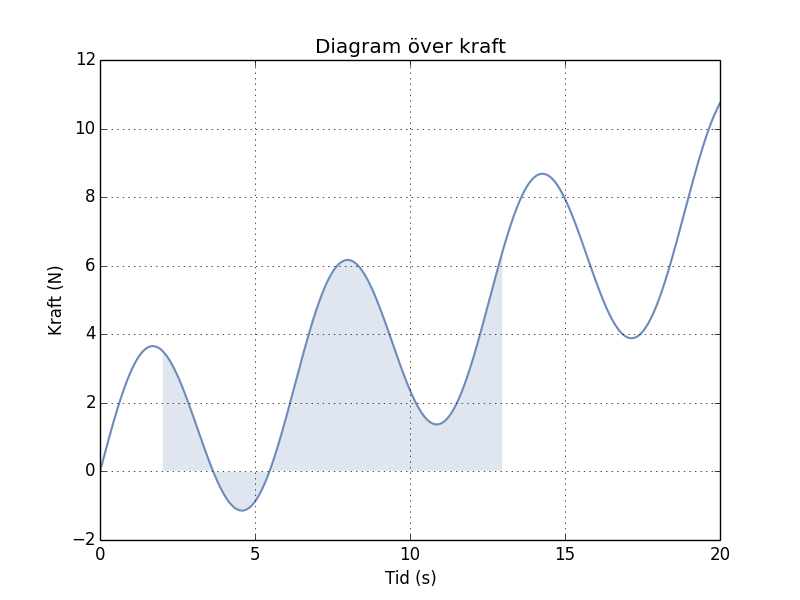
Matematisk ställs det upp som en integral över kraften från \(t_1\) till \(t_2\).

\[ I = \int_{t_1}^{t_2} F(t) dt\]

Funktionen \(F(t)\) är känd, likaså gränserna. Integralen som ska beräknas

\[ I = \int_{2}^{13} {3\sin{t} + 0.4t}~dt. \]

Primitiva funktioner av \(\sin{t}\) och \(0.4t\) beräknas eller hämtas ur tabell.

\[ I = \Big[- 3\cos{t} + 0.2t^2 {\Big]_2^{13}}\]

Värdena sätts in i den primitiva funktionen.

\[ I = (- 3\cos(13) + 0.2\cdot{13}^2) - (- 3\cos(2) + 0.2\cdot{2}^2)\]

Sätt in i räknaren och beräkna ett numeriskt värde,

\[ I = 29.0292...\approx 29~\text{Ns.}\]

Nästan alla grafräknare har en inbyggd numerisk lösning för integraler. Om du har en sådan kan du glatt sätta in funktionen och gränserna för att sedan låta räknaren ta hand om resten.