SVT-triangeln
SVT-triangeln är en enkel bild som en kan rita upp för att hålla koll på hur man räknar ut sträckan, hastighet eller tiden. Den fungerar helt enkelt så att man lägger tummen eller något finger på det man vill beräkna och då visar triangeln vilken beräkning som ska genomföras. Det blir sannolikt enklare med ett exempel.

- \(s\) är sträckan
- \(v\) är hastigheten
- \(t\) är tiden
Nedanstående exempel är inte ovanliga problem på nationella provet i årskurs 9 i matematik.
Beräkna tid med hjälp av SVT-triangeln
Hur lång tid tar det att köra Stockholm till Göteborg om bilvägen är 480 km lång och bilföraren håller en medelhastighet på 80 km/h?
Vi läser i uppgiften att det är tiden som ska beräknas. Då tar vi vår triangel och lägger för tummen på tiden.

Med hjälp av tummen ser vi nu att formeln för tiden skrivs
\[ t = \frac{s}{v}.\]
Vi använder formeln ovan med våra värden på sträckan och hastigheten.
\[ t = \frac{480}{80} = 6~\text{timmar.}\]
Bilresan tar således 6 timmar att köra för bilföraren.
Beräkna sträcka med hjälp av SVT-triangeln
Kajsa har fått i uppgift att mäta avståndet mellan Nynäshamn och Gotska Sandön. Dessvärre är avståndet för långt för att mätas med linjal, däremot har hon en segelbåt som kan segla i. Hon seglar med en medelhastighet på 9 km/h och kommer fram efter 10 timmar. Hur långt är det mellan Nynäshamn och Gotska Sandön?
Det är uppenbart att sträckan ska beräknas i uppgiften. Vi placerar vår tumme på sträckan som i figur 3 och kan nu enkelt skriva ner formeln för sträcka.
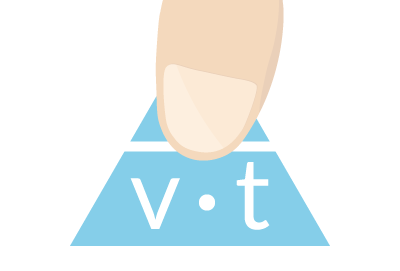
Formeln ges av SVT-triangeln och blir:
\[ s = vt\]
Vi har hastigheten och tiden given, och kan därför sätta in de i formeln.
\[ s = 9\cdot10 = 90~\text{km}.\]
Avståndet mellan Nynäshamn och Gotska Sandön bör då vara ungefär 90 kilometer om vi antar att hon seglar någorlunda rakt.
Trianglar för andra fysiska forlmer
Det är givetvis möjligt att konstruera en liknande triangel för alla samband som ser likadana ut. Det är således möjligt för exempelvis acceleration som skrivs som \(a=vt\), resulterande kraften \(F=ma\), eller arbetets \(W=Fs\). Vi rekommenderar dock att SVT-triangeln är den enda triangeln du lär dig och istället lär dig att lösa ut variabler ur formler, och de flesta formlerna står ju i en formelsamling.
Ingen kommer dock hindra dig från att göra det om du vill.