Elastisk stöt

Hej! I denna guide kommer vi att gå igenom ett exempel på en elastisk stöt. Det kan tidigare vara bra att ha koll på rörelsemängd och rörelseenergi, då det är det vi kommer att använda oss av i denna uppgift.

Två lådor som stöter i varandra

Nedanstående är två lådor som är påväg rakt mot varandra. Stöten är elastisk. Vi vill beräkna hastigheten på lådorna efter stöten. Detta kommer vi att göra genom att vi vet att både rörelsemängd och rörelseenergi bevaras i en elastisk stöt. Uppgiften som skall lösas är vilken hastighet lådorna får efter stöten i figur 1.

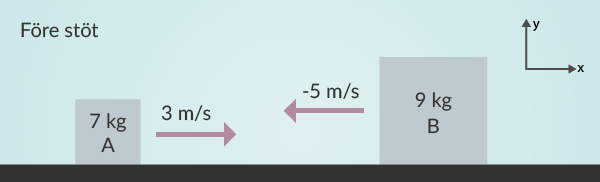
Vi ritar även upp en bild hur det ser ut efter stöten, mest för att göra det extra tydligt vad som händer. Massorna för respektive låda döps till \(m_A = 7~kg\) och \(m_B=9~kg\). Hastigheterna före stöten kallar vi \(v_{A1} = 3~m/s\) åt höger respektive \(v_{B1} = 5~m/s\) åt vänster.

Efter stöten kommer varje låda ha en ny hastighet. Dessa kallar vi för \(v_{A2}\) och \(v_{B2}\).

Uppgiften är således att lösa \(v_{A2}\) och \(v_{B2}\).

Lagen om rörelsemängdens bevarande gäller, så rörelsemängden före stöten är lika med rörelsemängden efter.

\[ \vec{\boldsymbol{p}}_{\text{före}} =\vec{\boldsymbol{p}}_{\text{efter}}\]

Minustecknena i uttrycket nedan kommer av att de åker mot riktningen som vi definierat som positiv uppe i högra hörnet. Samma håll som x-pilen är positivt, motsatt håll är negativt.

\[ m_A v_{A1} + m_B(-v_{B1}) =  m_A(-v_{A2}) +m_Bv_{B2}\]

Efter det gäller vår andra ekvation, rörelseenergin är bevarad.

\[ \text{Rörelseenergi före} = \text{Rörelseenergi efter}\]

Här behöver vi inte tänka på någon riktning då rörelseenergi inte är någon vektor, även om vi skulle tänka på riktning så försvinner den då hastigheten är i kvadrat i varje term.

\[ \frac{m_Av_{A1}^2}{2} + \frac{m_Bv_{B1}^2}{2} =  \frac{m_Av_{A2}^2}{2} +\frac{m_Bv_{B2}^2}{2}\]

Nu kommer vi att göra en avstickare en del lärare inte uppskattar (medan andra tycker det är trevligt). Vi kommer lösa det numeriskt istället, dvs, med värden på massorna och hastigheterna insatta. Våra ekvationer med numeriska värden insatta ger således.

\[ \begin{cases} 7\cdot3 + 9\cdot(-5) =  7(-v_{A2}) +9v_{B2} \\[1em] \frac{7 \cdot 3^2}{2} + \frac{9 \cdot 5^2}{2} = \frac{7v_{A2}^2}{2} +\frac{9v_{B2}^2}{2}  \end{cases}\]

Utför lite multiplikationer och summera ihop termerna.

\[ \begin{cases} -24 = -7v_{A2} +9v_{B2} \\[1em] 144 = \frac{7v_{A2}^2}{2} + \frac{9v_{B2}^2}{2} \end{cases}\]

Taktiken nu är att lösa ut \(v_{B2}\) ur den övre ekvationen och sedan sätta in den i den undre för att skapa en ekvation med en okänd. Flytta över \(-7v_{A2}\) till högerledet och dividera med \(9\) ger följande ekvationssystem.

\[ \begin{cases}  \frac{7v_{A2}-24}{9} = v_{B2} \\[1em] 144 =  \frac{7v_{A2}^2}{2} +\frac{9v_{B2}^2}{2} \end{cases}\]

Den översta raden substitueras nu in i den undre, och vi får följande ekvation att lösa.

\[ 144 =  \frac{7v_{A2}^2}{2} +\frac{9{(\frac{7v_{A2}-24}{9})}^2}{2}\]

Med hjälp av lite räkneregler förenklar vi uttrycket. Det finns många vägar att gå, en del expanderar kvadraten först, andra förenklar bråken först. Välj den väg du anser smidigast.

\[ 144 =  \frac{56v_{A2}^2}{9} - \frac{56v_{A2}}{3} + 32\]

Härifrån är lösningen densamma som för en andragradskevation. Vill vi lösa med pq-formeln kan vi fortsätta några steg till genom att subtrahera \(144\) från båda sidorna.

\[ 0 =  \frac{56v_{A2}^2}{9} - \frac{56v_{A2}}{3} - 112\]

Multiplicera alla faktorer med \(\frac{9}{56}\) för att göra faktorn framför kvadraten till \(1\).

\[ 0 =  v_{A2}^2 - 3v_{A2} - 18\]

Lösning med pq-formeln från Matematikguiden.se ger två rötter.

\[ \begin{cases}  v_{A2}  = 6 \\v_{A2} = -3 \end{cases}\]

Den första lösningen är den vi är intresserad av, för \(-3\) är fallet före stöten. Vi kan nu enkelt beräkna \(v_{B2}\) genom en tidigare ekvation.

\[ \frac{7v_{A2}-24}{9} = v_{B2}\]

Sätt in \(v_{A2} = 6\) i uttrycket.

\[ \frac{7\cdot6-24}{9} =  v_{B2}\]

Nu är vi färdiga och har hastigheten för vardera låda.

\[ v_{B2} = 2\]

Svar: Efter stöten rör sig låda A med en hastighet på 6 m/s åt vänster, medan låda B rör sig med hastigheten 2 m/s åt höger.

Alternativ uppställning

En alternativ uppställningsmetod är att strunta i vilken riktning båda lådorna har efter stöten och identifiera det efteråt. I princip antar vi att alla hastigheter är positiva efter stöten. Får de ett negativt värde efteråt är de på väg åt vänster. Lagen om rörelsemängdens bevarande skrivs som

\[ m_A v_{A1} + m_Bv_{B1} = m_Av_{A2} +m_Bv_{B2}.\]

Notera frånvaron av minustecken i själva uppställningen. Rörelseenergins bevarande skrivs som vanligt som

\[ \frac{m_A v_{A1}^2}{2} + \frac{m_B v_{B1}^2}{2} = \frac{m_A v_{A2}^2}{2} +\frac{m_B v_{B2}^2}{2}\]

Ekvationssystemet som nu ska lösas är:

\[ \begin{cases} 7\cdot3 + 9\cdot(-5) =  7v_{A2} +9v_{B2} \\[1em] \frac{7 \cdot 3^2}{2} + \frac{9 \cdot 5^2}{2} =  \frac{7v_{A2}^2}{2} +\frac{9v_{B2}^2}{2} \end{cases}\]

Detta system har lösningen:

\[ \begin{cases}v_{A2} = -6 \\ v_{B2} = 2 \end{cases}\]

Eftersom \(v_{A2}\) är negativ är lådan på väg mot vänster, medan det positiva \(v_{B2}\) talar om att den lådan är på väg mot höger.

Båda uppställningarna ger precis samma svar. Personligen föredrar skribenten den senare uppställningen. Det är lämpligt om du väljer den du tycker är bäst.

Räkneuppgift med jobbigare siffror

Siffrorna ovan gav ett mycket bekvämt och vackert svar. Låt oss anta att låda A nu har en massa på 6.89 kg och rör sig till höger med hastigheten 6.54 m/s. Låda B har massan 8.33 kg och rör sig med hastigheten 5.03 m/s åt höger. Hur stor är hastigheterna efter en elastisk stöt?

Svar: Låda A rör sig till vänster med en hastighet på 6.12 m/s och låda B rör sig till höger med en hastighet på 5.44 m/s.

Liknande uppgifter kan säkert dyka upp på prov eller dylikt. Det svåraste brukar inte vara att ställa upp uppgiften utan att lösa ekvationerna som blir.