Centripetalkraft
Centripetalkraft får vi om vi ersätter acceleration i Newtons andra lag med uttrycket för centripetalacceleration.
\[ F = m\frac{v^2}{r}\]
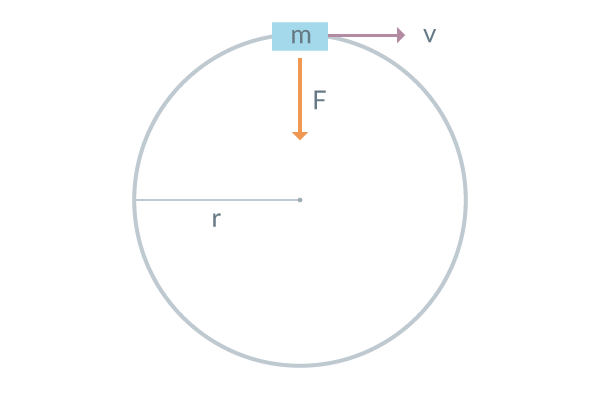
Ett exempel är om en bil kör in i en rondell med konstant hastighet. Bilens hastighetsmätare kommer inte ändras, däremot kommer riktningen att ändras, och det är centripetalkraften som ändrar riktningen.
Enheten är givetvis samma som för vilken annan kraft som helst, det vill säga 1 Newton.
Precis som med Newtons andra lag är inte centripetalkraften någon "egen" kraft, utan det är summan av de andra krafterna som är lika med centripetalkraften. Detta blir mycket tydligare om du läser vårt exempel på en loop.
Exempel på centripetalkraft
Ett svenskt vägmästerverk, Volvo XC90 har en massa på 2750 kg. Volvon kör in i en rondell med radien 20 meter och håller hastigheten 50 km/h, hur stor centripetalkraft verkar då på bilen? Bortse från alla andra påverkande faktorer.
Vi inleder med att konvertera hastigheten till m/s.
\[ v = \frac{50}{3.6} = 13.888...~\text{m/s.}\]
Nu kan vi sätta in våra värden i formeln.
\[ F = 2750\cdot\frac{13.888...^2}{20} = 26523~\text{N}~\approx 27~000~\text{N.}\]
Exempel på centripetalkraft i en loop
Ronny och hans kompisar är inte riktigt krya i skallen, så en kall vinternatt bestämmer de sig för att åka pulka ner i en loop de har byggt av snö. Loopen har en radie på 5.0 meter, Ronny har en massa på 77 kg inklusive pulkan och han står 14 meter över nollnivån. Hur stor normalkraft verkar på Ronny och pulkan när de är upp-och-ner i loopen?
Vi försummar friktion, hastighetsförluster och andra påverkande faktorer. För att underlätta ritar vi en bild. Ronny och pulkan har här ersatts av en gul låda för att göra det hela lite smidigare.
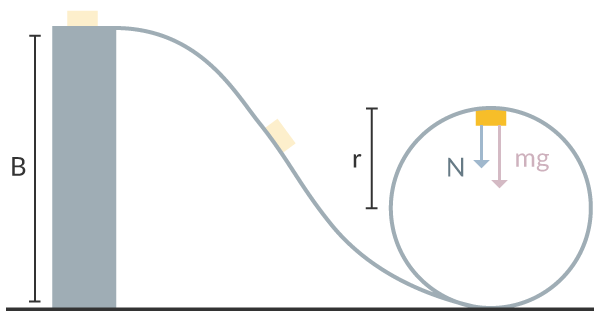
Nu kan vi sätta upp och summera våra krafter. Dessa är tyngdkraften och normalkraften. Dessa bildar den resulterande kraften som i detta fall är centripetalkraften. Normalkraften är riktad nedåt då det är en kontaktkraft mellan pulkan och loop-konstruktionen.
\[ N + mg = m\frac{v^2}{r}\]
Vi flyttar över tyngdkraften till högerledet då vi är intresserade av normalkraften.
\[ N = m\frac{v^2}{r} - mg\]
Med lite faktorisering blir uttrycket snyggare eller jobbigare beroende på hur man känner.
\[ N = m(\frac{v^2}{r}-g)\]
Nu kommer steg två i uppgiften, massan, radien och tyngdaccelerationen vet vi, men hastigheten är okänd. Detta kan vi ta reda på med hjälp av energiprincipen. All potentiell energi från att Ronny befinner sig på en höjd ska omvandlas till rörelseenergi, och ur rörelseenergin kan vi beräkna hastigheten.
\[ mgh = \frac{mv^2}{2}\]
Vi tecknar ett uttryck för höjden i loopens högsta punkt.
\[ h = B - 2r\]
Massan finns med på båda sidorna och kan således divideras bort, därefter kan vi multiplicera upp 2 och få loss hastigheten i kvadrat.
\[ 2g(B-2r) = v^2\]
Hastigheten i kvadrat substitueras in i vår formel för normalkraften och nu är vi nästan framme.
\[ N = m(\frac{2g(B-2r)}{r}-g)\]
Vi fyller nu i alla siffror i vår formel för normalkraft och beräknar värdet.
\[ N = 77\cdot(\frac{2\cdot9.82\cdot(14-2\cdot5)}{5} - 9.82) = 453.684... ~\text{N} \approx 450~\text{N.}\]
En normalkraft på ungefär 450 Newton verkar således på Ronny och pulkan då han är högst upp i loopen.