Hydrostatiskt tryck
Formeln för hydrostatiskt tryck kan skrivas som
\[ p = p_0 + \rho g h\]
Där \(p\) är det absoluta trycket, \(p_0\) lufttrycket, \(\rho\) är densiteten på vätskan, \(g\) är tyngdacceleration och \(h\) är djupet, eller höjden på vätskepelaren ovan. Lufttrycket \(p_0\) för jorden vid havsnivå och är ofta satt till \(101325~\text{Pa}\).
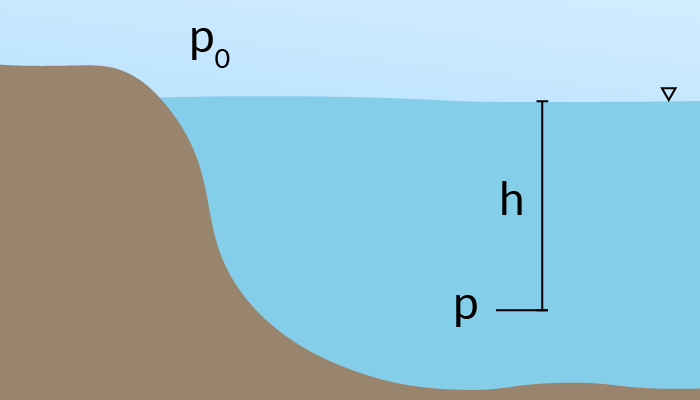
Det här med att trycket ökar på djupet känner du säkert igen från när du dyker ner i havet på sommaren, desto djupare desto mer trycker vattnet på dig och i öronen.
Den lilla triangeln används ibland för att markera var vätskans yta börjar. I bilder som figur 1 ovan med färg är det väldigt tydligt var gränsen går men i svartvita skisser kan det vara svårt att se, och då är triangeln viktig att rita dit.
Vattentryck & Vätsketryck
Andra lite mer alldagliga ord för hydrostatiskt tryck är vätsketryck och vattentryck. I det senare ordet menar vi givetvis specifikt vätskan vatten men beräkningarna fungerar på precis samma sätt oavsett.
Exempel på hydrostatiskt tryck
Titanic vilar på 3784 meters djup. Om en expedition planerar att besöka henne, vilket tryck behöver de dimensionera farkosten för?
Vi nyttjar formeln för hydrostatiskt tryck ovan.
\[ p = p_0 + \rho g h\]
För \(p_0\) använder vi lufttrycket för havsnivån, dvs \(101325~\text{Pa}\). Densiteten \(\rho\) för vatten sätter vi till \(1000~\text{kg}/\text{m}^3\) för enkelhetens skull. Tyngdaccelerationen \(g\) använder vi som brukligt \(9.82~\text{m}/\text{s}^2\). Till sist sätter vi djupet \(h\) enligt uppgiften till \(3784\).
\[ p = 101325 + 1000\cdot9.82\cdot3784\]
Slår vi in detta på en räknedosa får vi
\[ p = 37260205~\text{Pa.}\]
Vi har tre värdesiffror och använder ett prefix.
\[ p \approx 37.3~\text{MPa}.\]
Om vi vill kan vi konvertera detta till atmosfär genom att dividera med \(101325\), för \(101325~\text{Pa} = 1~\text{atm}\).
\[ p = \frac{37260205}{101325} \approx 368~\text{atm}.\]
Enligt våra räkningar bör trycket nere i Titanic således vara ungefär 368 gånger så stort som lufttrycket. Den här siffran kan variera då luftrycket, densiteten och tyngdaccelerationen är uppskattade variabler.
Ta reda på djupet med hjälp av en tryckmätare
En manometer är en anordning som mäter tryck. En dykare kan med hjälp av en sådan bestämma vilket djup denne befinner sig på. Om dykarens tryckmätare visar det absoluta trycket \(300~\text{kPa}\), vilket djup befinner sig denne på?
Vi ställer upp formeln för hydrostatiskt tryck. Vi vill lösa för djupet \(h\).
\[ p = p_0 + \rho g h \]
Subtrahera \(p_0\) från båda leden.
\[ p - p_0= \rho g h \]
Dividera med \(\rho g\).
\[ h = \frac{p - p_0}{\rho g}\]
Vi kan sätta in våra numeriska värden. Glöm inte \(10^3\) för prefixet kilo.
\[ h = \frac{300\cdot10^3 - 101325}{1000\cdot9.82} \]
Vi får ett ungefärligt numeriskt svar,
\[ h = 20.23...~\text{m.}\]
Dykaren befinner sig på ungefär 20.2 meters djup.
Hydrostatiskt tryck på en annan himlakropp
Kraken Mare är ett hav på Saturnus måne Titan som består av mestadels flytande ammoniak. Om vi designar en rymdsond med en liten undervattensrobot på som ska kunna dyka ner till 30.0 meters djup för att ta prover, hur stort tryck behöver vi dimensionera roboten för då?
Vi behöver lite data om Titan, i tabeller kan vi hitta att lufttrycket är \(146.7~\text{kPa}\), tyngdaccelerationen \(1.352~\text{m}/\text{s}^2\) och densiteten på flytande ammoniak är \(422~\text{kg}/\text{m}^3\).
Precis som innan startar vi med formeln för hydrostatiskt tryck,
\[ p = p_0 + \rho g h. \]
Därefter behöver vi identifiera vad som är vad i datan given ovan. Det första är lufttrycket, detta är \(p_0\), således
\[ p_0 = 146.7~\text{kPa.}\]
Efter det har vi \(\rho\), vilket är densiteten. I detta fall ska roboten sänkas ner i ammoniak vilket betyder att
\[ \rho= 422~\text{kg}/\text{m}^3.\]
Då vi befinner oss på en annan himlakropp har vi en annan tyngdacceleration än jorden, den är given,
\[ g = 1.352 ~\text{m}/\text{s}^2.\]
Till sist vet vi att roboten ska dyka ner 30.0 meter, då kommer den ha en vätskepelare på 30.0 meter vilket betyder att
\[ h = 30.0~\text{m}.\]
Allt detta sätter vi in i formeln,
\[ p = 146.7\cdot 10^3 + 422\cdot 1.352\cdot 30.0.\]
Sätt in i en miniräknare och vi har ett numeriskt svar,
\[ p = 163816.32~\text{Pa} \approx 164~\text{kPa}.\]
Således behöver vi dimensionera roboten för \(164~\text{kPa}\), och sedan kan det kanske vara lämpligt att lägga till lite säkerhetsmarginal ovanpå detta.