Potentiell energi i en fjäder

Den potentiella energin, fjäderenergin som finns lagrad i en fjäder som är förskjuten från jämviktsläget $x$ meter kan skrivas som

$$E_k = \frac{kx^2}{2}$$

där $E_k$ är energin i joule, $k$ är fjäderkonstanten i $N/m$ och $x$ är ihoptryckningen eller utdragningen i meter.

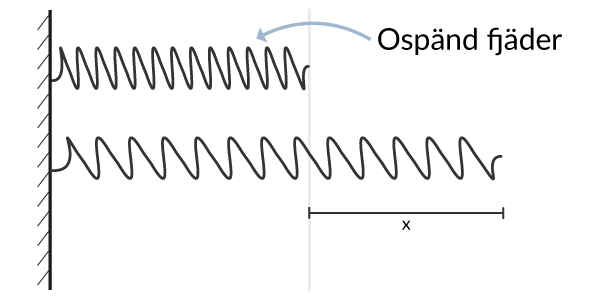
Detta gäller under förutsättningen att fjädern inte dragits ut eller tryckts ihop så pass mycket att den deformerats och gått sönder. Om fjädern inte återgår till sitt ospända läge har den sannolikt deformerats permanent.

Exempel på beräkning av energi i en fjäder

En fjäder har med fjäderkonstanten 39 N/m dras ut 0.67 m. Hur mycket energi finns då lagrad i fjädern? Om den dras ut den dubbelt så långt, hur mycket energi finns då lagrad i fjädern?

Vi nyttjar formeln ovan,

$$E_k = \frac{39\cdot{0.67}^2}{2} = 8.75355 \approx 8.8~\text{J.}$$

Om vi drar ut den dubbelt så långt multiplicerar vi $x$ med $2$.

$$E_k = \frac{39\cdot{(2\cdot0.67)}^2}{2} = 35.0142 \approx 35~\text{J.}$$

Energin blir alltså fyra gånger så stor om vi drar ut fjäderns dubbelt så långt. Detta kommer av $x^2$-termen. Nu tittar vi på hur vi kan använda en fjäder för att sätta fart på en leksaksbil.

Skjuta iväg en leksaksbil med hjälp av fjäderenergi

En fjäder med fjäderkonstanten 356 N/m är fastsatt i en vägg. En leksaksbil med massan 707 gram pressas in i fjädern så att den trycks ihop 5.10 cm, vilken fart får bilen när den släpps?

Vi inleder med en figur över situationen.

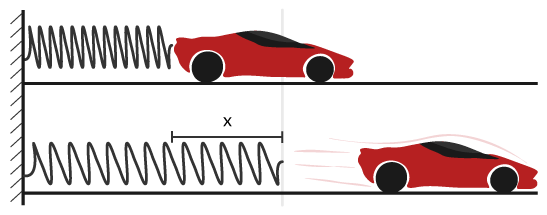
Vi sätter upp en likhet, all fjäderenergi när den pressas ihop ska omvandlas till rörelseenergi hos leksaksbilen.

$$\text{Potentiell energi i fjädern} = \text{Rörelseenergi hos bilen}$$

Vi sätter in uttrycken för respektive energi.

$$\frac{kx^2}{2} = \frac{mv^2}{2}$$

Vi kan direkt stryka divisionen med $2$ i båda leden.

$$kx^2 = mv^2$$

Dividera med massan $m$ på båda sidorna.

$$\frac{kx^2}{m} = v^2$$

Nu kan vi dra roten ur båda uttrycken för att få reda på vilken fart bilen får.

$$v = \sqrt{\frac{kx^2}{m}}$$

Sätt in våra siffror ovan och utvärdera ett numeriskt svar. Glöm inte att konvertera centimeter till meter och gram till kilogram.

$$v = \sqrt{\frac{356\cdot 0.051^2}{0.707}} \approx 1.14~\text{m/s.}$$

Detta är en hyfsat vanlig typ av uppgift gällande fjäderenergi, energin som finnas lagrad i fjädern ska skjuta en kula, bil eller tvärtom, en bil kör in i en fjäder och ihoptryckningen är sökt.