Sträcka-tid-graf till och från affären på cykel

Hej! Idag fortsätter vi och tittar på en till graf-uppgift. Förra gången kikade vi på en hastighet-tid-graf och nu är det dags för sträcka-tid-grafen, ofta kallad st-diagram, st-graf eller liknande.

I figur 1 nedan finns sträckan från Adam och Bertils hem given som funktion av tiden. Adam startar hemifrån på cykel och Bertil startar på cykel från affären i samma ögonblick.

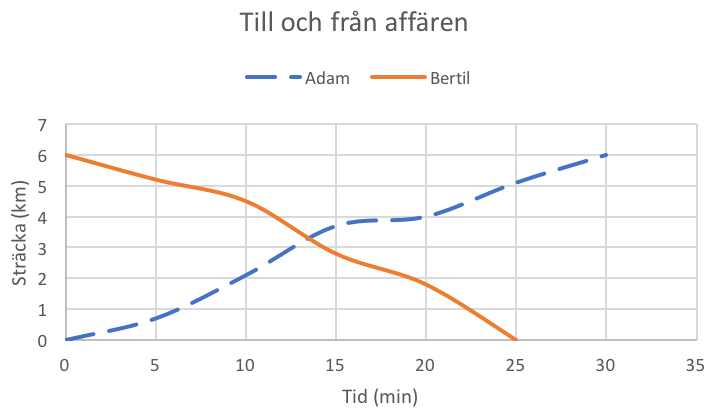
Frågorna vi vill besvara är:

• När möts de?
• Vem har högst medelfart?
• På vägen till affären finns det en jobbig backe, baserat på grafen, var är det rimligt att den är placerad?

När möts de i s-t-diagrammet?

Adam och Bertil bör mötas då de befinner sig på samma avstånd från hemmet eller från affären. Detta inträffar när linjerna korsar varandra. Således träffar Adam och Bertil varandra vid strax över 3 kilometer och ungefär 14 minuter efter att Adam lämnat hemmet och Bertil affären.

Vem har högst medelfart?

Båda herrarna har avverkat sträckan 6 km, men de har gjort det på olika tid. Vi nyttjar formeln för medelhastighet.

\[ v = \frac{s}{t}\]

Här nyttjar vi ordet fart istället för hastighet då vi inte är intresserade av att de cyklar åt olika håll.

Adams medelfart

\[ v = \frac{6}{30} = 0.2~\text{km/min}\]

Bertils medelfart

\[ v = \frac{6}{25} = 0.24~\text{km/min}\]

Den som trampar snabbast på sin cykel är därmed Bertil.

Var finns backen påväg till affären?

I en backe bör det bli jobbigare att cykla och hastigheten bör då gå ner något. Hastigheten ser vi i ett sträcka-tid-diagram som lutningen på kurvan. Vid ungefär 4 kilometer har Adam det riktigt tungt och hans hastighet är nära 0 då lutningen är nära 0. Tvärtom ser vi att Bertils kurva börjar luta mer och då ökar hans hastighet, vilket är rimligt om han cyklar nerför en backe.

Vi drar slutsatsen att med denna information bör backen vara placerad 4 kilometer från hemmet eller 2 kilometer från affären.