Rörelsemängd - massa multiplicerat med hastighet
Hej! På denna sida går vi igenom rörelsemängd inom gymnasiets fysikkurser, alldeles från början. För rörelsemängd gäller kort och gott massan multiplicerat med hastigheten.
\[ \vec{\boldsymbol{p}}= m\vec{\boldsymbol{v}}\]
Där \(p\) är rörelsemängden, \(m\) är massan på objektet och \(v\) är objektets hastighet Då rörelsemängd är en vektor (har storlek och riktning), har vi markerat vad som är vektorer genom att göra de feta och rita dit en pil ovan. Ofta ignoreras detta på grund av lathet eller att det anses uppenbart.
Enhet för rörelsemängd
Enheten för rörelsemängd är
\[ p = 1~kg\frac{m}{s}.\]
vilket uttalas "kilogram meter per sekund". Ofta skrivs den som \(p = 1~kgm/s\).
Exempel på rörelsemängd och vektorer
En bil med massan 1500 kg kör med hastigheten 20 m/s. Vi definierar en positiv riktning, allt åt höger på skärmen eller pappret är positivt, och allt åt vänster är negativt. I figur 1 visas bilens rörelsemängd när den är på väg åt höger.

När bilen sedan kör åt andra hållet är rörelsemängden negativ, vilket visas i figur 2.
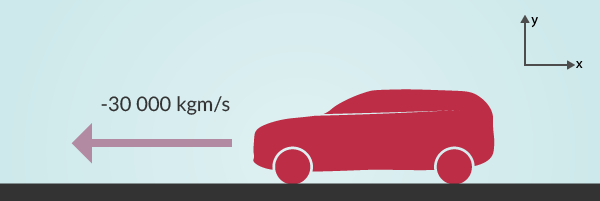
När vi ritar figurer håller vi koll på att alla pilar som är samma som vår positiva riktning uppe i hörnet är positiva, och alla som är riktade åt andra hållet är negativa. Det är väldigt viktigt att hålla koll på vart ett föremål är på väg, lagen om rörelsemängdens bevarande nedan blir omöjlig att använda annars.
Lagen om rörelsemängdens bevarande
Om inga yttre krafter påverkar ett system är dess rörelsemängd konstant. Detta kallas lagen om rörelsemängdens bevarande , ibland kortare benämnt som rörelsemängdslagen . Detta innebär att vi kan titta på systemets rörelsemängd före någonting inträffar (exempelvis kollision) och efteråt. Dessa måste vara lika med varandra. I våra beräkningar kan vi skriva något av följande stil.
\[ \vec{\boldsymbol{p}}_{\text{före}} =\vec{\boldsymbol{p}}_{\text{efter}}\]
Ett exempel skulle kunna vara ett system som inkluderar två stycken fordon med given rörelsemängd. Om dessa skulle kollidera i varandra kommer systemet fortfarande ha samma rörelsemängd, medan bilarnas hastighet kan ha förändrats.
Exempel på en kollision av ovan finns på stötar och kollisioner.
Skillnad på rörelsemängd och rörelseenergi
Rörelsemängd är en vektor, vilket betyder att vi vet hur hur stor den är, samt vilken riktning den har, medan rörelseenergi är en skalär, som vi inte alls vet var den är på väg någonstans.
Om vi exempelvis definierar att positiv riktning är åt höger, så kommer en bil som åker åt höger ha en positiv rörelsemängd. Om samma bil istället kör åt vänster kommer den ha en negativ rörelsemängd. Om vi kikar på bilens rörelseenergi är denna densamma oavsett åt vilket håll bilen kör.
Det går att beräkna rörelseenergi ur rörelsemängd. Detta med hjälp av formeln nedan.
\[ E_k = \frac{p^2}{2m}\]
För att avgöra vad det är för typ av stöt används både rörelseenergi och rörelsemängd.
Stötar & kollisioner
Det finns tre typer av stötar, elastisk stöt, oelastisk stöt och fullständigt oelastisk stöt. För att få plats med alla exempel har vi flyttat ut stötar till en separat sida. Vi har en knapp nedan som tar dig dit omedelbart.
Länk till stötar och kollisioner
Impulslagen
Impuls är ändringen av rörelsemängd. Exempelvis kan en rymdraket ändra sin rörelsemängd med hjälp av att en kraft verkar under en tid. Det enkla uttrycket för impuls, vid en konstant kraft ser ut som följande.
\[ I = F \Delta t=p_2 - p_1\]
Det finns även en mer generell version av impuls som säger att impulsen är lika med arean under grafen i Ett kraft-tids-diagram. Detta och en rad exempel finnes på sidan som är länkad nedan.