Vilken påskhare är snabbast?
Denna genomgång skrevs som ett blogginlägg påskafton 2017 och kanske inte riktigt är anpassad för att fungera som en fristående guide.
Hej! Idag påbörjas en uppgift i tre delar. Idag, påskafton kommer den första ut, på påskdagen kommer del 2 och den spännande upplösningen publiceras på annandag påsk. Det hela kommer handla om att läsa grafer för hur två olika påskharars hastighet varierar med tiden. Vi kommer beräkna acceleration med hjälp av derivata och sträcka med hjälp av integration.
Tidigare kan det vara bra om du läst om hastighet och acceleration.
Påskharen vs Påskharen 3000
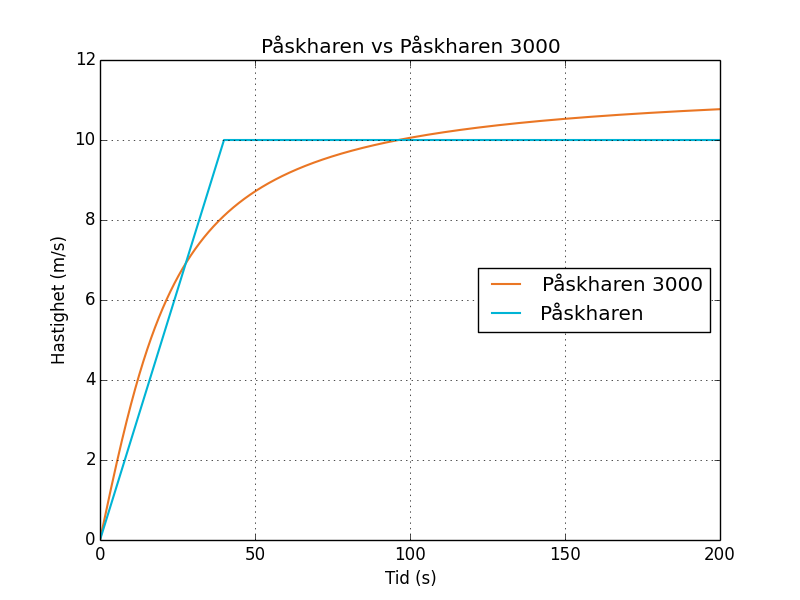
De ansvariga för påsken har funderat på att uppgradera den nuvarande Påskharen till en ny version, nämligen Påskharen 3000. I Figur 1 har hastigheten för Påskharen (blå) och Påskharen 3000 (orange) ritats upp som funktion av tiden. Påskharen 3000s hastighet kan beskrivas matematiskt med hjälp av den inversa tangensfunktionen.
\[ v_{3000}(t) = \frac{23}{\pi}\arctan\Big(\frac{t}{20}\Big),~t > 0.\]
Den inversa tangensfunktionen har några matematiska egenskaper som kommer underlätta arbetet. Dess primitiva funktion och derivata är följande:
\[ \int A\arctan\Big(\frac{t}{B}\Big)dt = A\Bigg(t\arctan\Big(\frac{t}{B}\Big)-\frac{1}{2}B\ln(B^2+t^2)\Bigg) + \text{konstant}\]
\[ \frac{d}{dt}\Bigg(A\arctan\Big(\frac{t}{B}\Big)\Bigg) = \frac{A}{B\Big(1+\frac{t^2}{B^2}\Big)}\]
Idag kommer vi att titta på tre frågor.
Påskaftonens frågor
- När har påskhararna samma hastighet?
- Vilken är den störa accelerationen påskharen har?
- Vilken acceleration har påskharen 3000 efter 40 sekunder?
När har påskhararna samma hastighet?
Detta kan vi avläsa grafiskt. Vi tittar i figur 1 efter punkter där linjerna i figur 1 korsar varandra. Där har de samma värde på y-axeln och således samma hastighet.
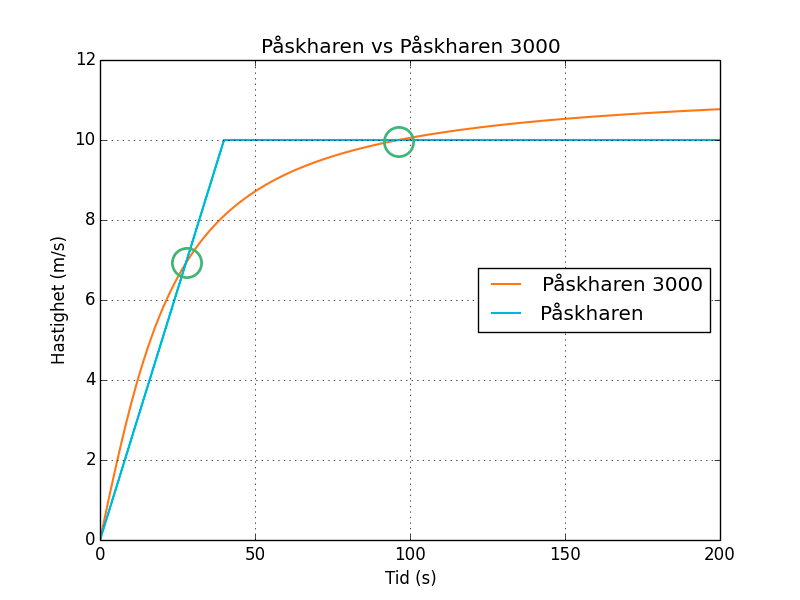
I figur 2 utläser vi två skärningspunkter som vi ringat in i grönt, den ena vid ungefär 25 sekunder och den andra vid runt 95 sekunder. Det exakta värdet är svårt att avläsa, så ett visst spann tillåts här. De exakta lösningarna är med sex värdesiffror 27.6736 sekunder och 96.2453 sekunder.
Vilken är den största accelerationen Påskharen har?
Accelerationen i ett hastighets-tidsdiagram är lutningen på kurvan. Påskharens acceleration är som störst under de första 40 sekunderna, och då har hastigheten ökat från 0 till 10 m/s. Lutningen på den konstanta accelerationen räknas ut genom dividera hastighetsförändringen på tiden.
\[ a = \frac{\Delta v}{\Delta t} = \frac{10-0}{40-0} = 0.25~m/s^2.\]
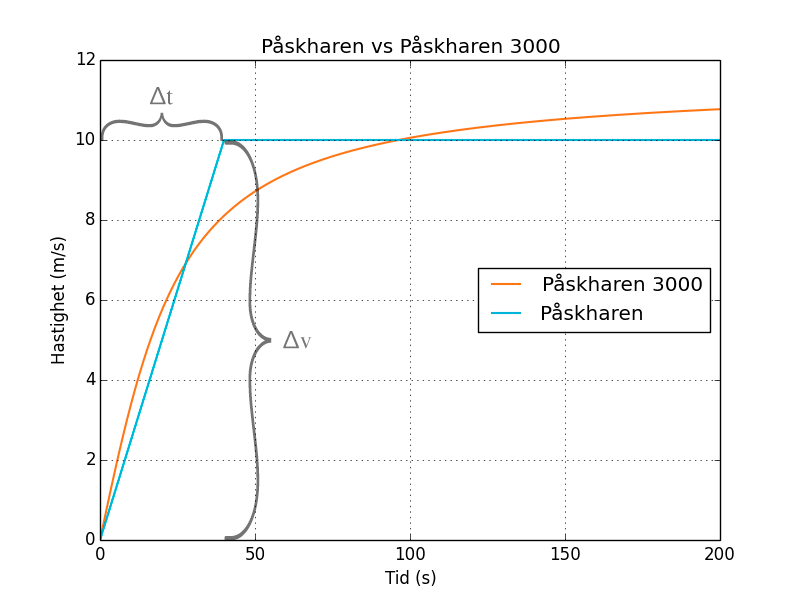
Den största accelerationen som påskharen har är således 0.25 m/s2. Det har den från tiden 0 sekunder till 40 sekunder, och därefter är accelerationen 0, då hastigheten är konstant.
Vilken acceleration har Påskharen 3000 efter 40 sekunder?
Precis som i förgående uppgift är accelerationen lutningen på kurvan. Det är möjligt att ta ut två punkter kring 40 sekunder och räkna ut lutningen på tangenten genom dessa, men detta är både knepigt och blir inte lika exakt som om vi deriverar. Med derivata får vi som bekant lutningen på en funktion. Vi deriverar med hjälp av att identifiera koefficienter och formeln given i början.
\[ a_{3000}(t) = v_{3000}'(t) =\frac{\frac{23}{\pi}}{20\Big(1+\frac{t^2}{20^2}\Big)}\]
Vi minns hur vi förenklar bråk.
\[ a_{3000}(t) =\frac{23}{20\pi\Big(1+\frac{t^2}{400}\Big)}\]
Vi är intresserade av accelerationen efter 40 sekunder.
\[ a_{3000}(40) =\frac{23}{20\pi\Big(1+\frac{40^2}{400}\Big)} = 0.0732113...~m/s^2.\]
Vi kan svara med hur många siffror som helst, men runt 0.07 m/s2 bör vara lagom. Missa inte den spännade uppföljningen i morgon, då tar vi om Påskharen 3000 någon gång har samma acceleration som Påskharen. Utöver detta räknar vi också ut vilken påskhare som kommer längst på 80 sekunder.