Hastighet-tid-graf till kraft-tid-graf
Hej! Idag ska vi titta på hur vi kan rita om ett hastighet-tid-diagram till kraft-tid-diagram. Låt oss formulera själva uppgiften.
Hastigheten på en bil med massan 1500 kilo återfinns i figur 1. Rita en graf över den resulterande kraften som funktion av tiden.
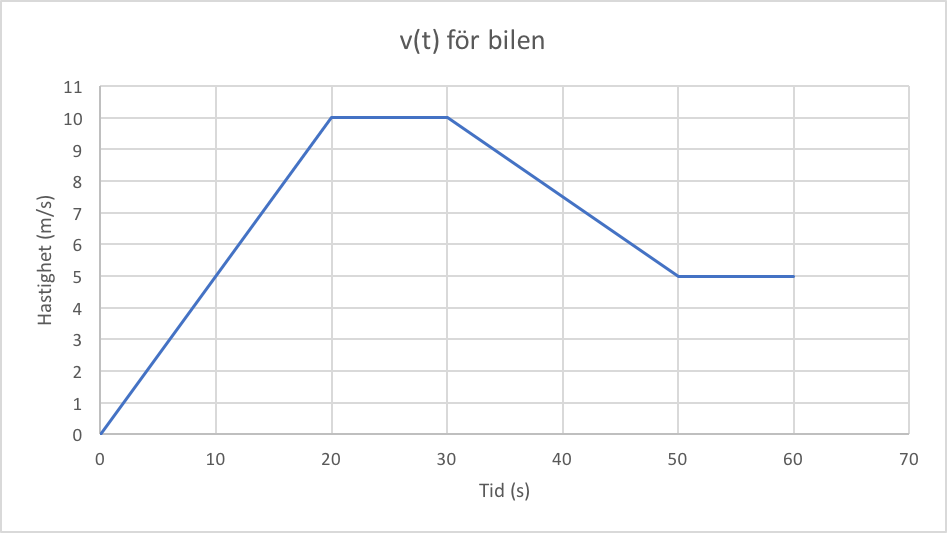
Målet är således att med hjälp av grafen i figur 1 rita en ny graf där vi har den resulterande kraften som funktion av tiden. Vi vill ha kraften på y-axeln och tiden på x-axeln.
Kort sagt kommer vi först att räkna ut accelerationen genom att det är lutningen på kurvan, och sedan nyttja Newtons andra lag för att ta reda på den resulterande kraften.
Accelerationen är lutningen i grafen
Nyckeln till hela uppgiften är att lutningen på kurvan i ett hastighet-tids-diagram är accelerationen. Mer om det finns under grafer.
Om vi delar upp kurvan i olika lämpliga intervall kan vi räkna ut accelerationen för var och en av dessa.
0 till 20 sekunder
Vi använder formeln
\[ a = \frac{\Delta v}{\Delta t} = \frac{v_2-v_1}{t_2-t_2}\]
för att räkna ut accelerationen. Detta går till på samma sätt som när vi räknar ut riktningskoefficienten för en linje vilket du kanske gjort i matematik 2.
\[ a = \frac{10-0}{20-0} = 0.5~\text{m}/{s}^2.\]
Vi fortsätter med nästa etapp.
20 till 30 sekunder
Nu är lutningen på grafen 0 eftersom den är helt horisontal. Vill vi ändå räkna ut det gör vi på samma sätt.
\[ a = \frac{10-10}{30-20} = 0~\text{m}/{s}^2.\]
30 till 50 sekunder
Vi fortsätter på samma sätt igen, men här ser vi att grafen lutar nedåt och vi förväntar oss då en negativ acceleration eftersom hastigheten minskar.
\[ a = \frac{5-10}{50-30} = -0.25~\text{m}/{s}^2.\]
50 till 60 sekunder
Även här är lutningen på grafen 0 och då följer det att accelerationen också är 0.
\[ a = \frac{5-5}{60-50} = 0~\text{m}/{s}^2.\]
Om vi vill vara riktigt snygga i texten kan vi skriva
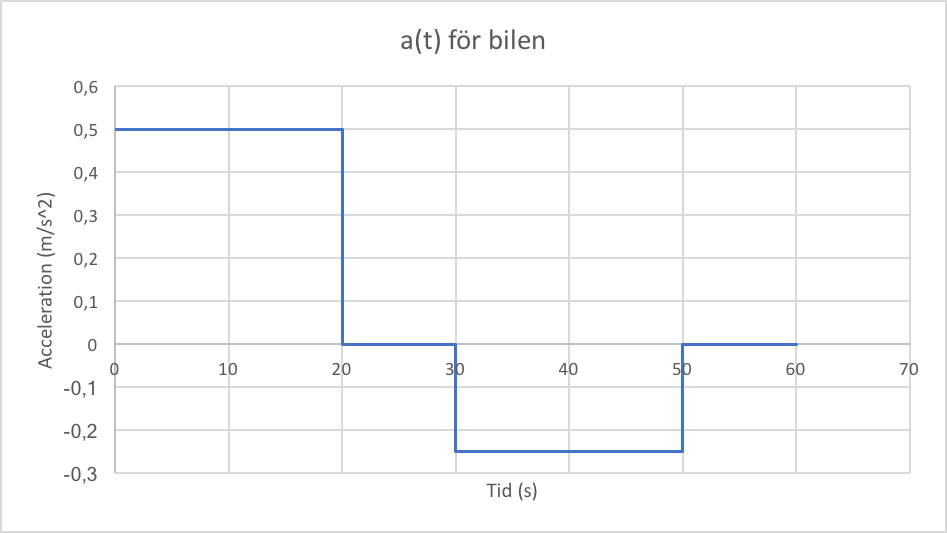
\[ a(t) = \begin{cases} 0.5 ~\text{m}/\text{s}^2 ~~~~ 0 \leq t \leq 20 \\ 0~\text{m}/\text{s}^2 ~~~~ 20\leq t \leq 30 \\ -0.25~\text{m}/\text{s}^2 ~~~~30 \leq t \leq 50 \\ 0~\text{m}/\text{s}^2 50 ~~~~ \leq t\leq 60 \end{cases}\]
Graf över acceleration som funktion av tiden
Nu ritar vi ut accelerationen som funktion av tiden i en graf. Då bör den se ut som figur 2.
Newtons andra lag för kraften
Den resulterande kraften hittar vi genom Newtons andra lag.
\[ F= ma\]
Vi använder vår fina ekvation ovan och multiplicerar med massan \(m=1500~\text{kg}\).
\[ F(t) = \begin{cases} 1500\cdot 0.5~\text{N} ~~~~ 0 \leq t \leq 20 \\ 1500\cdot 0~\text{N} ~~~~20 \leq t \leq 30 \\ 1500\cdot(-0.25)~\text{N} ~~~~ 30 \leq t \leq 50 \\ 1500\cdot 0~\text{N} ~~~~50 \leq t\leq 60 \end{cases}\]
Utför varje multiplikation och vi är framme vid kraften för varje tidsintervall.
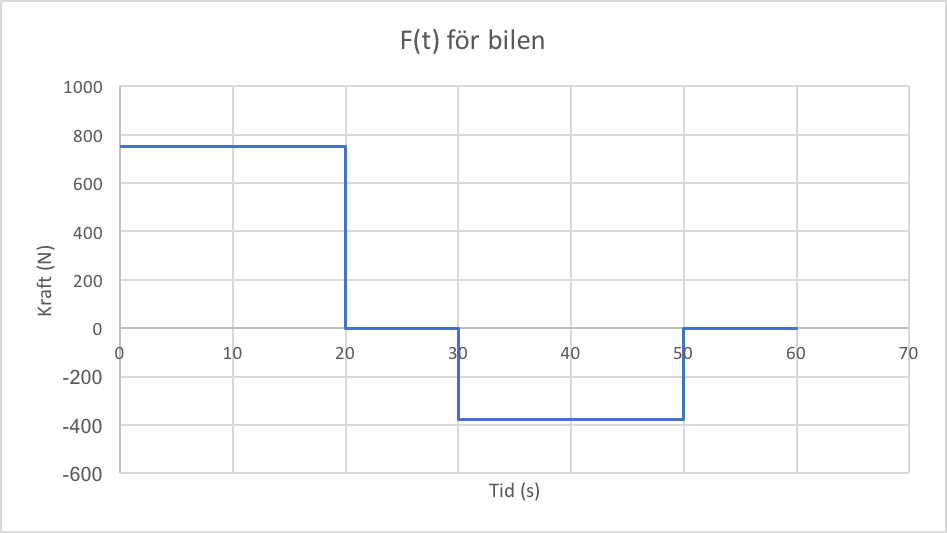
\[ F(t) = \begin{cases} 750~\text{N} ~~~~ 0 \leq t \leq 20 \\ 0~\text{N} ~~~~ 20 \leq t \leq 30 \\ -375~\text{N} ~~~~ 30 \leq t \leq 50 \\ 0~\text{N} ~~~~ 50 \leq t\leq 60 \end{cases}\]
Kraften som funktion av tiden
Nu ritar vi in kraften som funktion av tiden och då är vi framme vid vårt slutgiltiga mål.
En kort repetition, vi har hastigheten som funktion av tiden och vill rita en graf över den resulterande kraften som funktion av tiden. Vi tar ut accelerationen genom att det är lutningen i en hastighet-tids-graf. Därefter räknar vi ut den resulterande kraften genom att det är massa multiplicerat med accelerationen.