Kraft i kätting på skylt
Hej! I denna exempeluppgift hjälper vi Victors Fiskdeli att beräkna hur stor kraften är i en kätting som håller upp en skylt. Följande uppgift förekommer ofta i skiftade skepnader, ibland är det en skylt som hänger på en balk med en lina, ibland är det en ljuslykta som hänger i en sned kätting, men de har alla liknande lösning med hjälp av tidigare kunskaper av komposantuppdelning och kraftmoment.
Victors Fiskdeli önskar sätta upp en skylt. Skylten hänger på en homogen balk som är 1.8 meter lång med massan 10.0 kg, fastsatt i en fiktionsfri led. Längst ut hänger själva skylten med massan 12.5 kg. Vinkeln mellan balken och kättingen är 25°. Hur stor är kraften i kättingen?
Först kommer vi att rita en enkel skiss över vilka krafter som verkar. Därefter delar vi upp kättingens kraft i två vinkelräta komposanter. Till sist nyttjar vi att för jämnvikt är summan av alla kraftmoment noll.
Rita en bild med alla krafter
Vi ritar ut alla krafter som verkar. I högra hörnet visar vi att positiv riktningar är uppåt och till höger, samt att ett kraftmoment medurs är positivt runt rotationspunkten A. Massan för balken betecknas \(m_b\). Massan för skylten kallar vi för \(m_s\) och kraften i kättingen döper vi till \(S\). Avståndet från väggfästet ut till skylten kallar vi för \(L\).
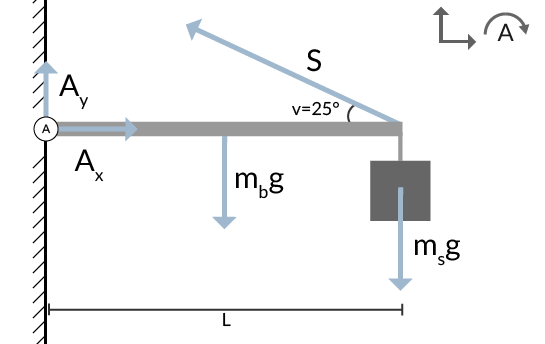
I den friktionsfria leden finns en horisontal och en vertikal lagerkraft. Ibland, händer det att en del exempeluppgifter och böcker hoppar över att rita ut dessa. Resultatet på kraften \(S\) blir inte fel om dessa ignoreras, men det blir inte riktigt rätt hela vägen fram.
Komposantuppdelning av kraften S
Ett kraftmoment består av en kraft och en vinkelrät sträcka. Vi måste dela upp kraften \(s\) så den är vinkelrät mot balken. Detta görs med hjälp av trigonometri och illustreras i figur 2.
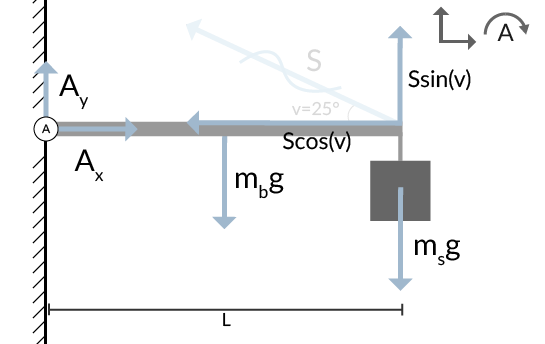
Summan av alla kraftmoment är noll
Vi kommer här ihåg att vi har definierat positiv riktning som medurs. Det betyder att alla kraftmoment som vill vrida balken medurs är positiva, och alla som vill vrida balken moturs är negativa.
Det första momentet kommer från själva balken, då den är homogen betyder det att den är lika tjock och har samma massfördelning överallt. Balkens tyngdpunkt är av detta skäl precis i mitten. Det andra momentet kommer från skylten som vill vrida balken nedåt och det sista från kättingen som vill vrida balken uppåt.
\(A_y\) och \(A_x\) ger inga kraftmoment eftersom dessa sitter i rotationspunkten, avståndet från dessa till rotationspunkten A är ju 0.
\[ 0 = m_bg\frac{L}{2} + m_sgL - S\sin{v}L\]
Längden \(L\) kan divideras bort.
\[ 0 = \frac{m_bg}{2} + m_sg - S\sin{v}\]
Flytta över \(S\sin{v}\) till vänsterledet.
\[ S\sin{v}= \frac{m_bg}{2} + m_sg\]
Divison med \(\sin{v}\) och var har ett uttryck för kraften \(S\).
\[ S =\frac{m_bg}{2\sin{v} } + \frac{m_sg}{\sin{v} }\]
Med våra numeriska värden insatta beräknas kraften till
\[ S = \frac{10.0\cdot9.82}{2\sin{25^{\circ}} } + \frac{12.5\cdot9.82}{\sin{25^{\circ}} }.\]
Detta slaget på en miniräknare ger
\[ S = 406.632... \approx 4.1 \cdot 10^2~\text{N}.\]
Svar: Kraften i kättingen är 4.1 · 102 Newton.
Beräkna reaktionskraften
Som extra bonus kommer vi beräkna reaktionskraften, dvs \(A_y\) och \(A_x\). Enligt första andra lag är summan av alla krafter för ett föremål som står still noll. Vår balk rör inte på sig, därför kommer vi applicera Newtons första lag i vertikalled respektive horisontalled.
Summan av krafter horisontellt
Positiv riktning är satt åt höger, alla pilar som pekar ditåt är således positiva och tvärtom.
\[ A_x - S\cos{v} = 0\]
Vi kan flytta över \(S\cos{v}\) till högerledet.
\[ A_x = S\cos{v}\]
Numeriska värden kan nu sättas in.
\[ A_x = 406.632\cdot\cos{25^{\circ}} = 368.534...\text{N.}\]
Summan av krafter vertikalt
Positiv riktning är satt uppåt.
\[ A_y + S\sin{v} - m_bg - m_sg = 0\]
Lös ut \(A_y\) genom att flytta över allt annat till högerledet.
\[ A_y = - S\sin{v} + m_bg + m_sg\]
Numeriska värden insatta.
\[ A_y = - 406.632\cdot\sin{25^{\circ}}+10.0\cdot9.82 + 12.5\cdot9.82 = 49.1~\text{N.}\]
Dessa krafter kan nu slås ihop. Detta kan göras med hjälp av Pythagoras sats.
\[ A = \sqrt{A_x^2 + A_y^2}\]
Vi har numeriska värden på båda krafterna, dessa kan vi sätta in
\[ A = \sqrt{368.534^2 + 49.1^2} = 371.79... \approx 3.7\cdot10^2~\text{N.}\]
Svar: Reaktionskraften är 3.7 · 102 Newton.