Fullständigt oelastisk stöt
Hej! Idag ska vi titta på ett exempel på en fullständigt oelastisk stöt. Du kanske tidigare läst om rörelsemängd, eller sett våra exempel på en elastisk stöt eller en oelastisk stöt.
En kanonkula med massan 15 kg skjuts med hastigheten 25 m/s in i en vagn med massan 140 kg som rör sig mot kulan med hastigheten 0.6 m/s. Kulan fastnar i vagnen. Hur stor är hastigheten för vagnen och kulan efteråt?
Metod för problemet
Vi vet att det är en oelastisk stöt, eftersom kulan och vagnen sitter ihop med varandra efteråt. De har således samma hastighet efter. Vi ritar först ut en bild och tittar på våra riktningar, sedan använder vi lagen om rörelsemängdens bevarande för att räkna ut den sammansatta kroppens nya hastighet.
Utförande och räkning
I figur 1 har vi illustrerat hur det ser ut innan stöten. Vi har tagit oss friheten att anta att vagnen åker åt vänster och kulan åker åt höger.
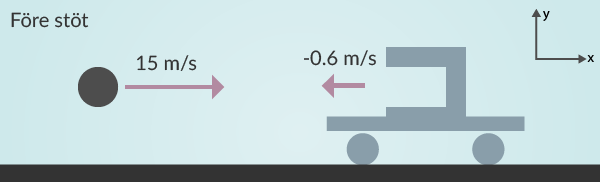
Det är viktigt att komma ihåg vad som är positiv riktning. Allt som rör sig åt höger är positivt, och allt som rör sig åt vänster är negativt vilket vi definierat i högra hörnet. Massan på kulan kallar vi \(m_k\), hastigheten på kulan \(v_k\). Massan och hastigheten på vagnen kallar vi \(m_v\) respektive \(v_v\). Den nya hastigheten båda har gemensamt kallar vi för \(v_2\).
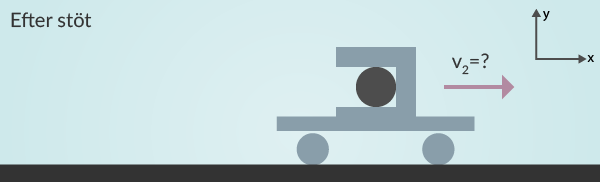
Nu är det dags att börja räkna. Vi inleder med att ställa upp lagen om rörelsemängdens bevarande.
\[ \vec{\boldsymbol{p}}_{\text{före}} =\vec{\boldsymbol{p}}_{\text{efter}}\]
För vårt problem ovan har vi följande rörelsemängder före och efter.
\[ m_kv_k + m_v(-v_v) = (m_k+m_v)v_2\]
Observera här att vi egentligen inte vet riktningen på \(v_2\). Vi har antagit att den är positiv, får vi ett positivt svar är antagandet korrekt och den sammansatta kroppen på väg åt höger, får vi ett negativt värde är den sammansatta kroppen på väg åt vänster. Dividerar vi med \((m_k+m_v)\) på båda sidorna får vi hastigheten vi söker ensam.
\[ \frac{m_kv_k + m_v(-v_v)}{(m_k+m_v)} = v_2\]
Numeriskt med våra värden insatta.
\[ v_2 = \frac{15\cdot25 + 140\cdot(-0.6)}{15+140} = 1.877..\approx 1.9~m/s.\]
Till sist rundar vi formellt av det med ett svar.
Svar: Vagnen rör sig åt höger med hastigheten 1.9 m/s.
Om vagnen och kulan hade kommit från motsatt håll, dvs vagnen kom från vänster och kulan från höger hade resultatet blivit att vagnen rörde sig åt vänster med en lika stor hastighet.
När v2 blir negativt
Låt oss anta att massan på vagnen istället är \(m_v = 1850~kg\), medan alla andra värden är densamma. Hur stor blir hastigheten för den sammansatta kroppen efter stöten då?
Vi nyttjar formeln rakt av för \(v_2\).
\[ v_2 = \frac{15\cdot25 + 1850\cdot(-0.6)}{15+1850} = -0.394...\approx -0.4~m/s.\]
Detta innebär att vagnen och kulan är på väg åt vänster, som vi ritat in i figur 3.
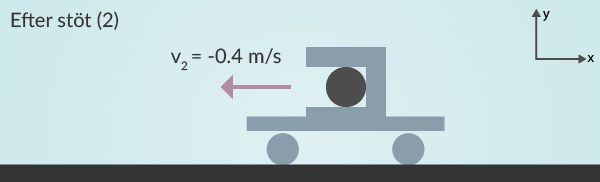
Detta visar varför det är viktigt att hålla koll på sina minus-tecken i beräkningar med vektorer, för ett minustecken ändrar riktningen helt.