Newtons gravitationslag för två chokladbollar i rymden
Hej! Idag firar vi chokladbollens dag. Detta givetvis med en chokladbollsrelaterad uppgift som börjar mycket mystiskt men det ordnar som vanligt upp sig i slutändan.
Två chokladbollar i rymden
Två sfäriska chokladbollar av samma smet med radien 2.8 cm och 2.5 cm hänger långt ute i rymden långt från andra påverkande himlakroppar med ett avstånd 40 cm från varandra. Kraften mellan chokladbollarna är 11.5 pF, vilken densitet har chokladbollarna?
Vi har nedan ritat en figur för att förtydliga situationen.
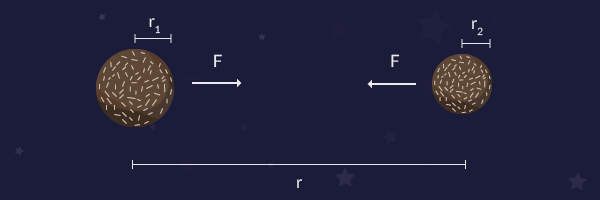
Figuren ovan är inte skalenlig på något vis, den är mer tänkt som ett stöd för förståelsen.
Newtons gravitationslag
Den första ledtråden till lösningen kommer från att vi vet att chokladbollarna hänger långt ute i rymden. Den enda kraften som påverkar chokladbollarna är den mellan varandra och den kan skrivas med Newtons gravitationslag.
\[ F = G\frac{m_1m_2}{r^2}\]
I uppgiften frågar de efter densiteten, och densiteten kan skrivas som massan multiplicerat med volymen.
\[ m = \rho V\]
Vi känner till volymen för ett klot,
\[ V = \frac{4}{3}\pi r^3.\]
Här kan det bli lite rörigt med variablerna, men \(r\) i den ovan avser vi på klotets radie, medan \(r\) i formeln för Newtons gravitationslag avser avståndet mellan deras masscentrum.
Vi sätter helt enkelt in detta i den första ekvationen och sedan ska vi försöka lösa för densiteten \(\rho\).
\[ F = G\frac{\rho \frac{4}{3}\pi r_1^3 \rho\frac{4}{3}\pi r_2^3}{r^2}\]
Uttrycket vi fått är allt annat än vackert, så vi passar på att snygga upp det lite.
\[ F = G\frac{(4\pi)^2 \rho^2 (r_1 r_2)^3}{(3r)^2}\]
Lös för \(\rho^2\).
\[ \frac{F(3r)^2}{G(4\pi)^2(r_1 r_2)^3} = \rho^2\]
Och till sist drar vi roten ur det hela.
\[ \rho = \sqrt{ \frac{F(3r)^2}{G(4\pi)^2(r_1 r_2)^3}}\]
Kvadraterna försvinner under rottecknet.
\[ \rho = \frac{3r}{4\pi}\sqrt{ \frac{F}{G(r_1 r_2)^3}}\]
Numeriskt värde för oss
Då \(G=6.672\cdot10^{-11} \text{Nm}^2/\text{kg}\) är det lämpligt om vi konverterar våra längdenheter till meter, då kommer vi få ut att densiteten har enheten \(\text{kg}/\text{m}^3\). Därifrån kan vi om vi vill omvandla till något lämpligare.
\[ \rho = \frac{3\cdot 0.4}{4\pi}\sqrt{ \frac{11.5\cdot10^{-12}}{6.672\cdot10^{-11}(0.028\cdot0.025)^3}}\]
Detta ger en densitet på
\[ \rho = 2140.65 ...\approx 2100~\text{kg}/\text{m}^3.\]
Då de flesta chokladbollarna inte är i storleksordningen av kilo eller kubikmeter kanske det är lämpligare att svara att chokladbollarna har densiteten 2.1 g/cm3.