När påskhararna sprungit samma sträcka?
Denna genomgång skrevs som ett blogginlägg annandag påsk 2017 och kanske inte riktigt är anpassad för att fungera som en fristående guide.
Hej! Vi hoppas du följt med både på påskafton och påskdagen och nu ser fram emot att lösa den sista uppgiften om påskhararna.
- Vid vilken tidpunkt har påskhararna sprungit lika långt?
Var förväntar vi oss att hitta lika tidpunkter?
Från påskaftonen tar vi figur 1 för de båda hararnas hastighet som funktion av tiden.
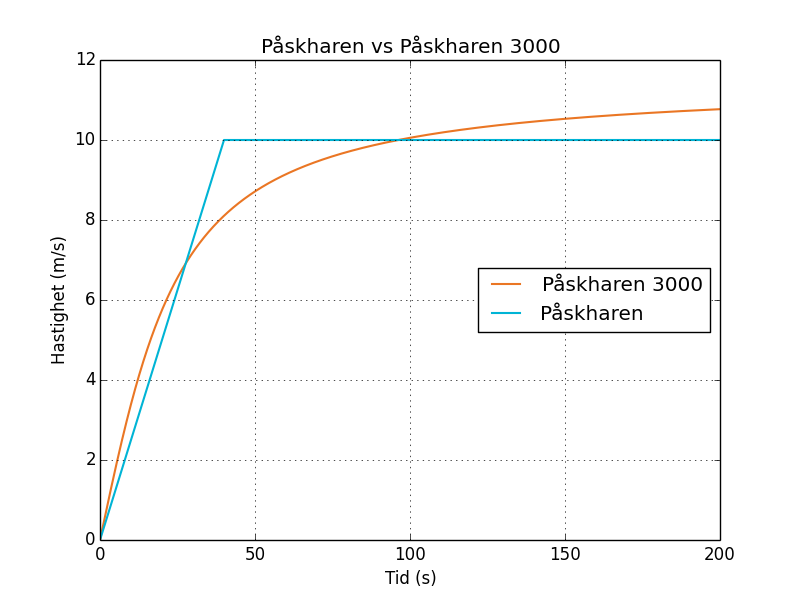
Vi kommer ihåg arean under kurvorna är respektive tillryggalagd sträcka. Fram till första punkten då de har samma hastighet är arean garanterat större för Påskharen 3000. Därefter växer arean för Påskharen snabbare. En kort stund efter 28 sekunder bör vi således ha en tidpunkt då de har sprungit lika långt.
Efter den andra tidpunkten då de har samma hastighet, 96 sekunder är Påskharen 3000s hastighet högre än Påskharens. Den bör således börja knappa in avståndet Påskharen har. Efter 96 sekunder bör vi således någonstans ha en punkt då hararna har sprungit lika långt igen.
Påskharen 3000s sträcka som funktion av tiden
Igår på påskdagen räknade vi ut hur lång sträcka Påskharen 3000 hade sprungit på 80 sekunder. Vi kan ersätta dessa 80 sekunder med en given tid \(t\) istället. Nu får vi sträckan Påskharen 3000 har sprungit i varje given tidpunkt.
\[ s_{3000}(t) =\int_{0}^{t} \frac{23}{\pi}\arctan\Big(\frac{t}{20}\Big) dt \]
Precis som igår använder vi den primitiva funktionen, men istället för den givna tidpunkten 80 sekunder sätter vi in i \(t\).
\[ s_{3000}(t) = \Bigg[\frac{23}{\pi}\Bigg(t\arctan\Big(\frac{t}{20}\Big)-\frac{1}{2}20\ln(20^2+t^2)\Bigg)\Bigg]_{0}^{t}\]
\[ \begin{split} $$s_{3000}(t) = \frac{23}{\pi}\Bigg(t\arctan\Big(\frac{t}{20}\Big)-\frac{1}{2}20\ln(20^2+t^2)\Bigg) - \\ \frac{23}{\pi}\Bigg(0\arctan\Big(\frac{0}{20}\Big)-\frac{1}{2}20\ln(20^2+0^2)\Bigg) \end{split}\]
Vi kan utvärdera den sista parentesen och snygga upp lite.
\[ \begin{split} $$s_{3000}(t) = \frac{23}{\pi}\Big(t\arctan\Big(\frac{t}{20}\Big)-10\ln(20^2+t^2)\Big) + 438.643 \\ \end{split}\]
Två intervall att söka i
Då funktionen som beskriver Påskharens hastighet inte är kontinuerlig, utan har en ramp upp och sedan tvärt övergår till att vara konstant måste vi dela upp sökningen i två intervall.
Grafisk lösning i intervallet 0 till 40 sekunder
I det första intervallet tittar vi på hur lång sträcka Påskharen har kommit medan den fortfarande accelererar.
Mellan 0 till 40 sekunder kan sträckan för konstant acceleration användas, och accelerationen har vi beräknat på påskaftonen.
\[ s_1(t) = \frac{0.25t^2}{2},~0 < t < 40.\]
Det vi gör nu är att vi ritar båda dessa funktioner och tittar på var de skär varandra, detta är ritat i figur 2.
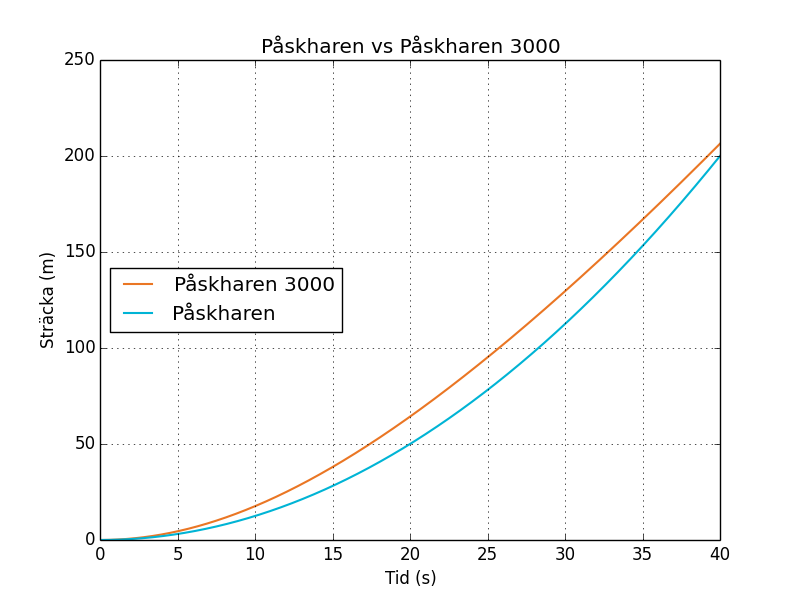
I figur 2 ser vi ingen skärningspunkt, av detta drar vi slutsatsen att det inte har sprungit lika långt någon gång under de första 40 sekunderna.
Grafisk lösning då tiden är större än 40
I intervallet 40 sekunder och över skrivs sträckan som
\[ s_1(t) = -200 + 10t,~t > 40.\]
\(-200\) är för att kompensera för de första 40 sekunderna. Vi ritar här upp funktionen från 40 till 300 sekunder för att se om vi hittar någon skärningspunkt. Låt inte detta orsaka någon tankevurpa. Om vi inte hade \(-200\) skulle vår funktion för sträcka göra ett hopp från \(200\) till \(400\) vid övergången, vilket givetvis är fel.
Nu ritar vi Påskharens sträcka-funktion för tider större än 40 sekunder, samt Påskharen 3000s sträcka-funktion. Lite på måfå har vi valt den övre gränsen 200 sekunder.
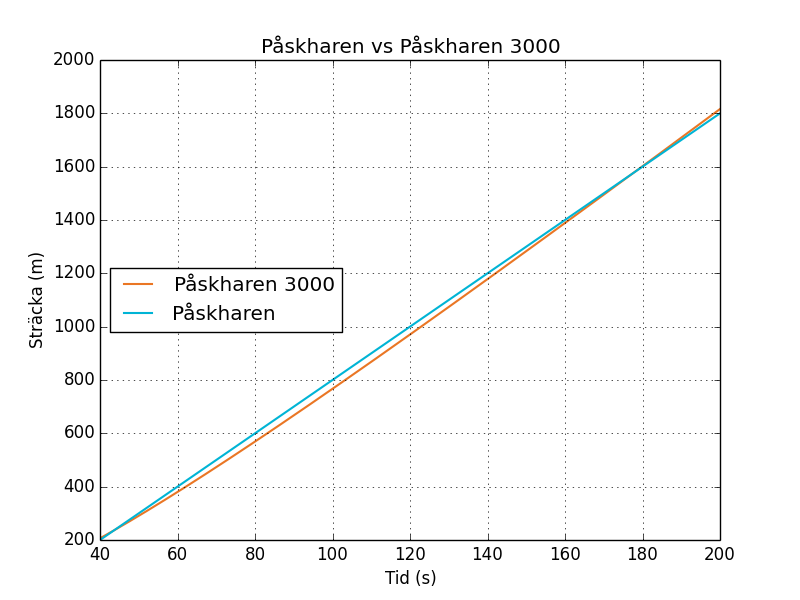
Vi tycks ana en skärningspunkt runt 40 sekunder och en runt 180 sekunder.
Om vi vill ha ett mer exakt värde kan vi zooma in runt dessa punkter. Vi ritar nu från 30 till 50 sekunder i figur 4.
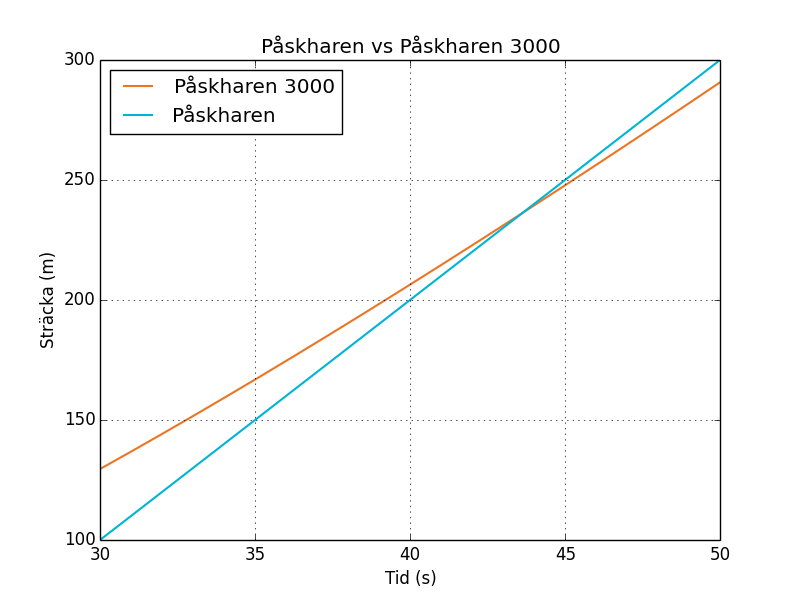
Nu är det tydligt att dessa skär varandra vid ungefär 43 sekunder.
Vi gör en till graf av funktionerna från 170 till 190 sekunder, vilket finns i figur 5.
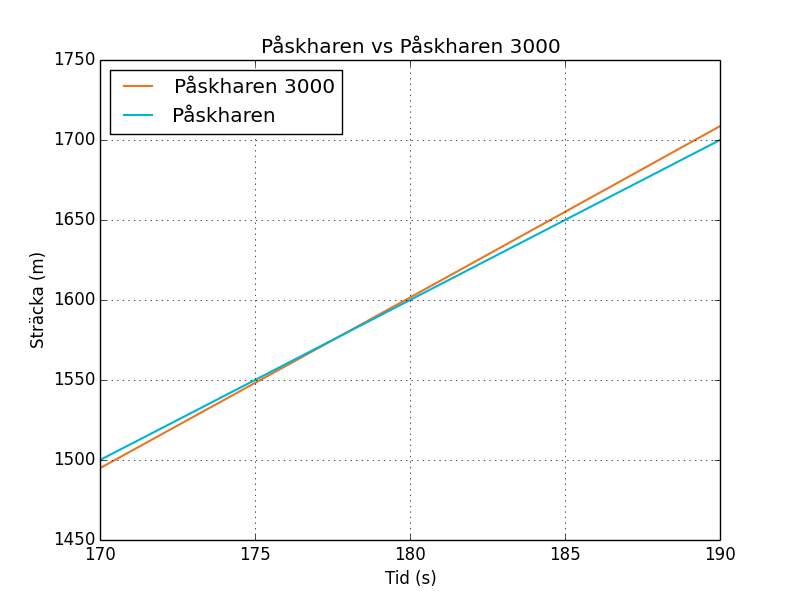
Vi ser en skärningspunkt vid ungefär 177 sekunder.
Med hjälp av graferna kan vi sammanfatta det som att hararna har sprungit lika långt vid två tidpunkter, en gång runt 43 sekunder och en gång vid 177 sekunder.
Numerisk lösning av skärningspunkter
Om vi har något datorhjälpmedel, eller en miniräknare med symbolhanterande kan vi lösa ut skärningspunkten numeriskt. Då vi redan vet att det inte finns några skärningspunkter i intervallet 0 till 40 sekunder fokuserar vi enbart på de två skärningspunkterna ovan.
Kort och gott går det till såhär,
\[ s_{3000}(t) = s_1(t).\]
Vi vill ta reda på när sträckan för dessa är lika och lösa ut tiden.
\[ \frac{23}{\pi}\Big(t\arctan\Big(\frac{t}{20}\Big)-10\ln(20^2+t^2)\Big) + 438.643 = -200 + 10t\]
Efter räkning får vi fram två tider,
\[ t_1 = 43.6163...\text{s}.\]
samt den andra tiden
\[ t_2 = 177.730...\text{s}.\]
Dessa stämmer väl överens med vår grafiska lösning. I många numeriska algoritmer kan beräkningstiden kraftigt minskas om en bra start-gissning finns, och om vi har gjort en bra grafisk lösning kan vi sedan givetvis använda den till den numeriska metoden.
En del program stannar dessutom efter de har hittat en lösning. På vår ekvation ovan skulle den exempelvis stoppa vid 43 sekunder, om vi däremot talar om för algoritmen att den måste leta kring 177 sekunder kommer den att hitta även den lösningen.